00098480

252 UL FUNKCJI ZMIENNEJ ZESPOLONEJ

Rozumując podobnie i korzystając z równości (111.37), otrzymamy

^<mw

przy czym symbole pochodnych cząstkowych we wzorach (111.38) j (111.39) oznaczają wartości tych pochodnych w punkcie (z*; y₀).

Porrtwnuiąc prawe strony równości (111.38) i (111.39), dostąjcmy ostatecznie du    dc    du    dc    ...

dx    dy    óy    dx

w punkcie (jt₀; y₀).

Równości (111.40) nazywają się warunkami (luh równaniami) Couchy’eg<h Riemama Udowodniliśmy zatem następujące twierdzenie.

Tw. JcUlt funkcja f(t) = u(x,y)+jv(x, y) ma w fmnkde z₀ ~ x₀ i jy₀ po-ct>,HŹną f(i₀), to pochodne cząstkowe

(tli^l)

_ _ ;

dy'dx ~5y

istnieją w punkcie (x_e; y₀) i spełniają warunki Cauchyego-Rtemanna (111.40).

Spełnienie pucz. pochodne cząstkowe (111.41) w punkcie (jr₀; y_Q) warunków (111.40), stanowi zatem warunek konieczny na to, żeby istniała pochodna/*(i₀). Pnyktai. Rozważmy funkcje/W ■“ Re «. Mamy tu

«<*. yi - *,    t(», y) - 0

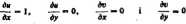
a zatem warunki Cauchy'e#o-Riemanna nie są spetniooe w ładnym punkcie płaszczymy. Wynika •tąd, te w ładnym punkcie ptezazyzay nie istnieje pochodna rozważanej funkcji.

Uwitą Aczkolwiek pochodna funkcji zmiennej zespolonej f(z) — Re a, czyli /Xs) — X, nie istnieje w ładnym punkcie płaszczymy, to jednakie pochodna funkcji zmiennej rzeczywistej /(*) — x istnŃje maywiŁio dla każdej (mezywatej) wartośd X. Przykład len ma na cefal wyrobienie u Czytelnika poflądu, te warunek istnienia pochodnej /'(*) jest warunkiem bardzo sOnytn, o czym przekonamy sic jeazem nie raz.

Istnienie pochodnych cząstkowych (UI.41) w punkcie (x₀; y_a) dwóch funkcji •K*. y) • «K*, y) i spełnienie przez te pochodne warunków Ca uchy'ego-Riemanna nie zapewnia istnienia pochodnej f(z₀) funkcji f(z) ~ u(x, y)+jo(x, y), a więc nie stanowi warunku wystarczającego na to, żeby pochodna/'(*b) istniała.

Pnykted. Niech

!1 dla xy — 0 0 dla xy p 0

a(x,y) ■e(x,y)-

Ponieważ

da    óu    de

bx    dy    ćx

0 w punkcie (0; 0)

więc pochodne cząstkowe (HMD istnieją i ipctniąją w punkcie (0; 0) warunki (ELSO). Wykażemy. że pochodna tomko, fi z) - m(x.y)+Mx,y) w tym punkcie nie istnieje. W tym celu

skorzystamy z definicji pochodnej (Ul.35) i z definicji Heinego granicy funkcji. Rozważmy zatem ci« (z.) zbieżny do zera, o wyrazach różnych od zera i taki, którego każdy wyraz o numerze nieparzystym łpeżrna warunek x,y. # 0, natomiast każdy wyraz o numerze parzystym spełnia warunek xj>. «= 0. Odpowiadający temu ciągowi {z.} ciąg

m

wartości ilorazu różnicowego 011.34) jest następujący

- -(*+■». 0, =ił±» 0, ...

Ponieważ założyliśmy, że lim z. « 0, więc otrzymany ciąg jest oczywiście rozbieżny, a zatem pochodna /'(O) rozważanej funkcji nie istnieje.

Za pomocą równań Cauchy'ego-Riemanna można zręcznie formułować różne warunki wystarczające na istnienie pochodnej /'(/,,) •

Warunek wystarczający istnienia pochodnej f'(z₀).

Tw. Jeżeli funkcje u(x,y) i o{x,y) są róiniczkowalne w punkcie (x„; y₀), a ponadto pochodne cząstkowe (111.41) spełniają w tym punkcie warunki (111.40), to funkcja f(z) =    y) ^ma pochodną f(z₀).

DOWÓD. Jeżeli funkcje tt(x, y) i »(*, y> są różniczkowali* w punkcie (_r₀: y„), to zacho-wując przyjęte poprzednio oznaczenia mamy

‘ ^ Ar-ł- ~ dy+o,(|d*|)	(IH.42)
> 4^- Ar + dy+p,(0z|) ix dy	(IU.43)

przy czym o,(|żi*!) i «i<UW) «4 «° nieskończenie małe rzędu wyższego niż Ufz|, gdy |d*i - iAx*+Ay* — 0

(por. część U, Str. 44). Skorzystamy teraz z warunków (III.40). Zastępując mianowicie w równości

da    ńe    de da    __,

(HL42)    — przez —oraz w równości (HL43) pochodną — praż —. a następnie

mnożąc obie strony równości (HL43) pras* ]. otrzymamy kolejno

Au — Ar— Ay+Oil\dx\)

jAo - /—Ar+> — dy+}oMaz\) W