052 053

52

Prz-ykład 2.6    -    |

Funkcje f<x_1tX2,Xj) * *1*2*^ ^{+ 5}1^X2^XJ ^{+ X}1*2^X3 ^{+ X}1^X2*3

zapisać « tablicy Karnaugha.

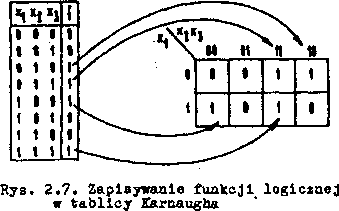
1)    Z tablicy zadanej funkcji przechodzimy natychmiast do tablicy Karnaugha (rys. 2.7).

2)    Funkcja składa się ze skład

ników ZNPS o numerach 2,3,4 i 7 i w tych kratkach wg numeracji z ry3. 2.6 wpisujemy Jedynki.    żt

Podstawową własnością tablicy Karnaugha jest łatwe rozpoznanie sąsiednich wyrażeń, podlegających sklejaniu. Z opisu wierszy i kolumn za pomocą kodu Gray'a wynika, że jedynkom (zerom) w kratkach przylegających do siebie bokami lub symetrycznych względem dowolnej z zaznaczonych na rys. 2.6 osi symetrii odpowiadają sąsiednie składniki ZNPS (czynniki ZNPI).

Zastanówmy się, jaki układ Jedynek w tablicy odpowiada implikantom prostym.

-    Składnikom ZNPS odpowiada w tablicy jedna jedynka.

-    Iloczynowi A nie zawierającemu jednej zmiennej r_Ł odpowiada para sąsiednich jedynek, bo powstaje on z dwóch sąsiednich składników ZNPS wg wzo-

,’U

A = Ax_ł + Ax_±

- Iloczynowi A nie zawierającemu dwóch zmiennych    odpowiada czwórka

jedynek, z których każda jest sąsiednia do dwóch innych, bo

A = A^ij ₊ Ai^j + A*^ ₊ A*_t*₃

-    Ogólnie, iloczynowi z którego usunięto k zmiennych, odpowiada grupa 2 jedynek, z których każda jest sąsiednia do k Innych z tej grupy.

-    Funkcji tożsamościowo równej 1 odpowiada tablica całkowicie wypełniona jedynkami.

Jak pamiętamy, implikant prosty to taki iloczyn, który nie da się już

Ir

uprościć. Jeżeli zatem w tablicy możemy utworzyć grupę zawierającą 2 jedynek i nie jest ona zawarta w grupie 2¹, 1 > k, Jedynek (czyli możemy otrzymać iloczyn pozbawiony k zmiennych, ale już nie możemy otrzymać iloczynu pozbawionego 1 zmiennych), to odpowiadający Jej iloczyn Jestimpli-kantem prostym.

Z powyższych i-ozważań wynika następująca metoda postępowania. Patrząc na tablicę Karnaugha wyszukujemy wszystkie, maksymalnych rozmiarów, grupy jedynek i otaczamy każdą z nich linią. Postępujemy w ten sposób aż do wyczerpania wszystkich Jedynek funkcji. Następnie przystępujemy do elimina-

9)

xf^V5 ^1z\ 000		001	111	010	HO	111	101	100
00		p	A	'T	Tj
01	(l	1	1	0	1J			D
11			1			"T	T
10		l^1	A			1	V

f»X₎X₂X₅łX_tX_(lX_5łXjX_{j t}X,X₅

l)

k)

Vi*	1 II	II	H	10	vx?ł	i 00	•i	«	10
1	®				0			(T	0
1		(i	0		1	Cl	0	j)

ł»*1*t*ł ^+xt*ł    f«x,x_Iłx{x₂*x,x_ł

o

c)

d)

,v* ^z\ ot		ii	«	to	x,X^	k ot	01	11	10
00	u	1	1	fi	01	SD	,'J		€
0(				1	01		0	(’1
11				1	11			U
10	r<	u	^1	Lu	10		“0

f*^xl*3V

f*T_t7₂x_t» *fy^xk * ^%l^xi^xk^ł *J*3

e)

i)

^ł\ W 01 H II

	U	>J
>)			'i

| = x₂x₎₍tx₂x_ł

\X,J *i*K	‘0 00	11	11	10
10
ot	Cl	0	J
11		n	0	0
10		U

{ = X|X₂Xj*X|XjX_ł»X₂XjX_i+X)X₂Xj

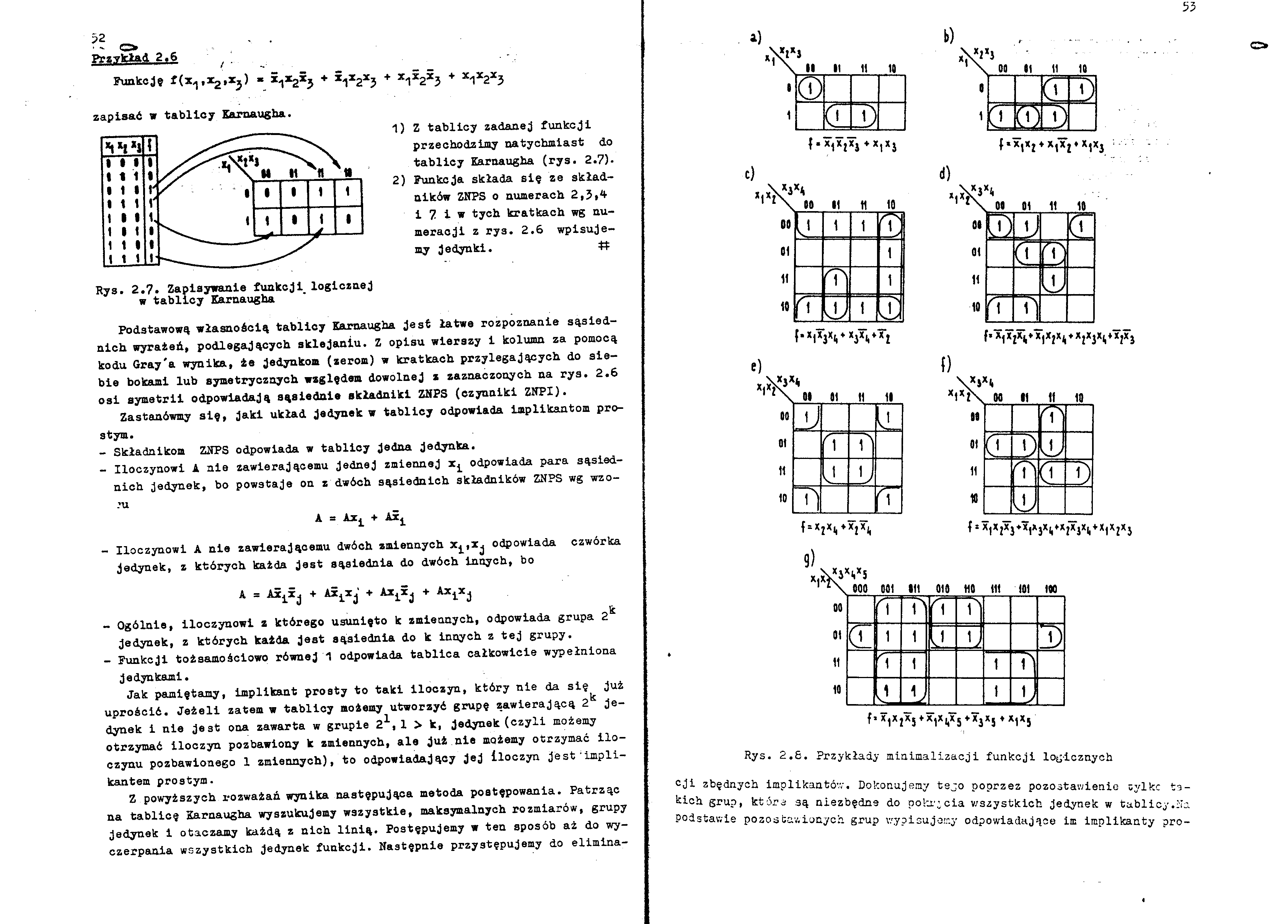
Rys. 2.6. Przykłady minimalizacji funkcji logicznych

cji zbędnych implikantów. Dokonujemy tejo poprzez pozostawienie tylkc takich stup, które są niezbędne do pokrycia wszystkich jedynek w tablicy,i!a Podstawie pozostawionych grup wypisujemy odpowiadające im implikanty pro-