0000090 (4)

teryzowania tego rodzaju procesu wprowadza się nową funkcję stanu zwaną entalpią //. Napiszemy równanie 4.5 w postaci

Q_P = (U_t+pVJ -M+pyj    4.6

wprowadzając oznaczenia

= U₂ + pV₂, H_l=U_l-\-pV₁ równanie 4.6 przyjmie postać

Q_p — H₂ — H₁ = A H    dla p = const    4.7

Funkcja

H=U + pV    4.8

jest funkcją stanu zwaną entalpią.

Przyrost entalpii AH jest równy ilości ciepła dostarczonego układowi w procesie izobarycz-nym Q_p = AH (przy p — const) tak, jak przyrost energii wewnętrznej A U jest równy ilości ciepła dostarczonego układowi iv procesie izochorycznym Q_v = At/ (przy V = const). Przykład. Jak zmieni się energia wewnętrzna 1 kg wody podczas wyparowania w temperaturze 373 K. i przy ciśnieniu 1 atm? Ciepło parowania wody w tych warunkach L = J l kcal\

= 22,6 • 10⁵ — ,( 540-), objętość 1 kg pary, objętość właściwa v = 1,725 m³/kg.

kg V kg /

N .

Parowanie odbywa się przy stałym ciśnieniu p = 1 atm = 101325 — , ciepło dostaniu”

czone L jest więc równe przyrostowi entalpii.

Uwaga. Energię wewnętrzną, entalpię, objętość odniesioną do jednostki masy (1 kg), oznaczać będziemy małymi literami jako energię wewnętrzną właściwą u, entalpię właściwą /;, wyrażające się w J/kg, względnie w cal/kg, oraz objętość właściwą v w m³/kg.

L = Mi = Av+pAv = 22,6 • 10⁵ -Ł ^540

Stąd przyrost energii wewnętrznej dla 1 kg:

Ah = A/i — pAr

Ile wynosi praca objętościowa pAr? Pomijając objętość właściwą wody ciekłej (10~³ m³/kg) w porównaniu z jej objętością w stanie lotnym (1,725 m³/kg) można przyjąć, że At) = 1,725 m³/kg. Wtedy

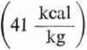
pAi = 101325 -^-m³

m3    |

1,725    = 1,74 ■ 10⁵ -j—

kg    kg

Wobec tego przyrost energii wewnętrznej podczas wyparowania 1 kg wody wynosi

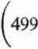
kcal \

kg J

97

Au = 22,6 ■ 10⁸    - 1,74 • 10⁵ ~ = 20,86 • 10⁵ /-

kg    kg    kg

7 — Podstawy biofizyki