CCF20090601009

x0	-4 2 ^0	1 2
X,	3 2 —X, 2 '	1 2
	3 2	1
^X2	~x2 2	?
^X3	-^x3 2 ^3	T 2
x4	3 2 2 ^Xą	1 ~2
^X5	^3-4 2 ^5	1 ^_2.

-1	1
3	1
5	25
1	11
5	25
1	11
5	~25
3	1
5	25
1	1

				"1 -1	1
				i -2 5 i -i 5 i i 5	1
1 1	1	1	1 1		25 11		6	0	6 5
-i -2	1	1	2 i		25 11	—	0	14	0
5	5	5	5					5
1 — L 25	11	11	— 1 25 J		25		6	0	1494
	25	25		, 2	1		_5		625 .
				5	25
				1 1	1

1

1	1	1	1
3	1	1	3
5	^_5	5	5
1	11	11	1
25	25	25	25

6a₀ H—a₂ =2

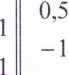
o

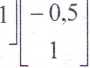
2

_7

5

18

5

6 a_n + — a, = 2

G p = b =>

=> a₂ =

-a, = —

a\ = —Vz,

6a₀ =2-—a₂

1494    18

-a-, = —

625    5

m=Pp„

151 11    5

—---1--<_ A--Ć,

210 70    14

1494    18

-=-

625 ‘    5

14

5

6

j^a» ⁺

-a₀ +

125

84~

	1	(	6	125^	1
	= —	2 -	— •		= -
	6	k	5	00 4^	28
1		125	P,	i	1	125	f 3 2	0	1
—	P\ ^4			—-	---X +		— X"	—	= -
2		84		28 2		84	u	2j	28

„ ,    151    11    5 ₂

f(x) =---H--H--X

210    70    14

+

1494    18

-a₂ = —

625 "    5

-£ +

5    5

n 125 +

84

3 f 2    1

--^ + -

2^5    5

y

2

10