CCF20091117�006


238 | CIĄGI
Obliczanie granic
Ćwiczenie A. Rozważmy ciągi określone wzorami: an = 4 + ^ oraz bn = 3 +
a) Oblicz lim an oraz lim bn.
n—co n—co
b) Niech c„ = an + bn i dn=an- b„. Zapisz wzory ciągów (c„) i (d„) i oblicz ich granice.
Poniżej podajemy własności granic, z których będziemy korzystać przy obliczaniu granic różnych ciągów.
Jeśli ciągi (a„) i (bn) są zbieżne, to zachodzą równości:
Jeśli ciągi (an) i (bn) są zbieżne i wyrazy ciągu (bn) są różne od O oraz lim bn 4 O, to:
n—co
lim (an + b„) = lim a„ + lim b„
n — oo n — co Al —00
i ■
lim r2- = n-°o bn
lim an
M —oo
lim bn
W—oo
lim (a„ - b„) = lim a„ - lim b„
n — oo n — co n —oo
Jeśh ciąg (a„) jest zbieżny i wszystkie jego wyrazy są nieujemne (an > 0), to:
lim (a„ ■ b„) = lim a„ ■ hm b„
n —oo n —oo n — oo
lim yojj =
n —oo
lim a
n —co
n
Zauważ, że z jednej z powyższych równości wynika, że dla dowolnej liczby rzeczywistej k, jeśli (an) jest ciągiem zbieżnym, to:
lim(k • a„) = k lim an
n—oo n — co
Wiemy już, jakie granice mają ciągi stałe oraz ciągi typu Wiadomo także, kiedy ciąg geometryczny jest zbieżny. W poniższych przykładach pokazujemy, jak korzystając z powyższych własności, można obliczać granice ciągów o bardziej skomplikowanych wzorach.
przykłady
lim (5 + -y - -7) = li
n-co V n5 n2 / n-
m 5 + lim - lim -^ = 54-0-0 = 5
-co n—co Y)-3 n—co Y)c
t
lim -4 = lim
17— co n—oo
7 • lim -V = 7 ■ O = O
n-co n2
lim
n-co
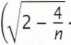
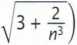
= lim
n—oo
2-
lim
n—co
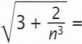
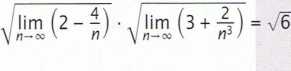
Wyszukiwarka
Podobne podstrony:
DSCN1124 (2) Rozważmy funkcje f:D -+ R i g:D -* R określone wzorami 10x /W-JJZT’ g(x) = 6-3x+i. Bada
CCF20090704�117 238 Część II określić, odwołując się do dwóch różnych tradycji: Arys-totelesowskiej
CCF20090831�131 238 Samowkdza z kolei znosi, ponieważ jest czymś określonym w porów-iS7 naniu z tym,
CCF20091117�000 230 CIĄGIGranice ciągów Ćwiczenie A. Oblicz sześć początkowych wyrazów ciągu określo
CCF20081203�067 (p = Fu Fx+F2 (Pgr (13.22) Wartości graniczne współczynnika napędu są określane dośw
CCF20091117�016 68 GRANICE FUNKCJI. POCHODNE Analogicznie określamy granicę właściwą funkcji w minus
skanuj0005 (238) Od autora jest utatwienie rozpoznania i określenia typu siedliska w praktyce urządz
img145 Granice błędu dla Y0 związane z losowością samego y oraz niedokładnością określenia parametró
więcej podobnych podstron