CCF20091202028

nosił zero, wartość mediany pozostałaby bez zmian, ale wartość średniej zmiejszyłaby się. Różnicę tę możemy sformułować następująco: zmiany wartości pomiarów ekstremalnych wpływają na wartość średniej, natomiast nie wpływają na wartość mediany dopóki nie zmienia się wartość pomiaru środkowego. W naszym przykładzie, dopóki 72 pozostaje trzecim pod względem wielkości pomiarem, mediana nie zmienia się.

Ta ważna różnica między miernikami umożliwia często decyzję w konkretnych przypadkach, których z dwu mierników jest właściwszy. Zwykle chodzi o to, by w obliczanym mierniku wykorzystać wszystkie dostępne informacje. Intuicyjnie mamy do takiej miary większe zaufanie, choć trudno to przekonanie uzasadnić statystycznie. Przytoczymy jednak kilka argumentów świadczących na korzyść średniej. Otóż miernik ten jest bardziej stabilny: jego wartość ulega mniejszym zmianom od próby do próby. Zastanawiając się nad problemami statystyki indukcyjnej przekonamy się, że badacz z reguły bardziej interesuje się populacją, z której pochodzi jego próba, niż samą tą próbą. Wie dobrze, że jeśli wybierze inną próbę, otrzyma nieco inne wyniki. Mając wiele prób, mógłby zbadać, jak dalece wartość średniej zmienia się przy zmianie próby. Otóż zaletą średniej jest to, że przy zmianie próby wartość mediany zmienia się bardziej niż wartość średniej. W praktyce pobieramy jednak zwykle tylko jedną próbę; warto więc wiedzieć, który miernik jest najbardziej rzetelny i przy przechodzeniu z jednej do drugiej próby wykazuje najmniejszą zmienność. Możemy więc sformułować następująca zasadę praktyczną: gdy mamy wątpliwości, raczej stosujemy średnią niż medianę.

Ale właśnie z racji swej zależności od wartości ekstremalnych, średnia może dać czasem wyniki bardzo mylące. Pamiętajmy, że pomiar tendencji centralnej polega na znalezieniu wartości pomiaru „typowej” dla danego zbioru. Posłużymy się krańcowym przykładem: niech najwyższy pomiar w serii 5 pomiarów omawianych wyżej wynosi 962. Medianą pozostanie 72, lecz średnia wyniesie 1241/5 == 248,2. Czy liczba ta jest w jakimkolwiek sensie „typowa” dla zbioru pomiarów? Oczywiście, nie! Nie jest bliska żadnemu z pomiarów. Z pewnością, żadnym pojedynczym miernikiem nie można opisać wartości typowego przypadku dla takiego zbioru pomiarów, ale 4 pomiary grupują się wokół wartości 72; zastosowanie mediany będzie w każdym razie mniej mylące. Możemy więc powiedzieć, że gdy rozkład jest silnie skośny, tj. gdy z jednej strony rozkładu jest wyraźnie więcej krańcowych pomiarów niż z drugiej, mediana jest miernikiem bardziej odpowiednim niż średnia.

Związek między skośnością rozkładu a względnym położeniem średniej i'mediany ukazuje rys. 5.1. Eksperymentalne wartości silnie wpływają na wartość średniej i przesuwają ją w kierunku wydłużonego skrzydła rozkładu. Kiedy rozkład jest całkowicie symetryczny, wartości średniej i mediany pokrywają się. Wiemy, że rozkłady dochodu są zwykle skośne: bardzo mała liczba bardzo wysokich dochodów powoduje wydłużenie skrzydła opisującego wysokie dochody. Dlatego podawanie średniego

symetryczn,

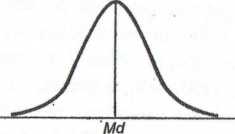
ujemnie skośny dodatnio skośny

Rys. 5.1. Związek między skośnością a względnym położeniem średniej i mediany.

dochodu w niewielkiej społeczności może być mylące. Stąd też dochody opisujemy raczej w kategjoriach mediany, niż średniej. Jeśli rozkład jest silnie skośny, fakt ten należy oczywiście uwzględnić w opisie danych. W takich przypadkach może być wskazane podanie i średniej i mediany, choć w praktyce rzadko się tak postępuje.

Średnia ma jeszcze jedną zaletę w porównaniu z medianą: jest wygodniejsza w operacjach algebraicznych. Czasem np. chcemy znaleźć średnią ważoną dla kilku grup danych. Mamy wartości średniego dochodu dla trzech społeczności, A, B i C.

&

Społeczność	Wielkość	Średnie
A	10000	3518
B	5000	4760
C	8000	4122

73