granica ciągu zadania

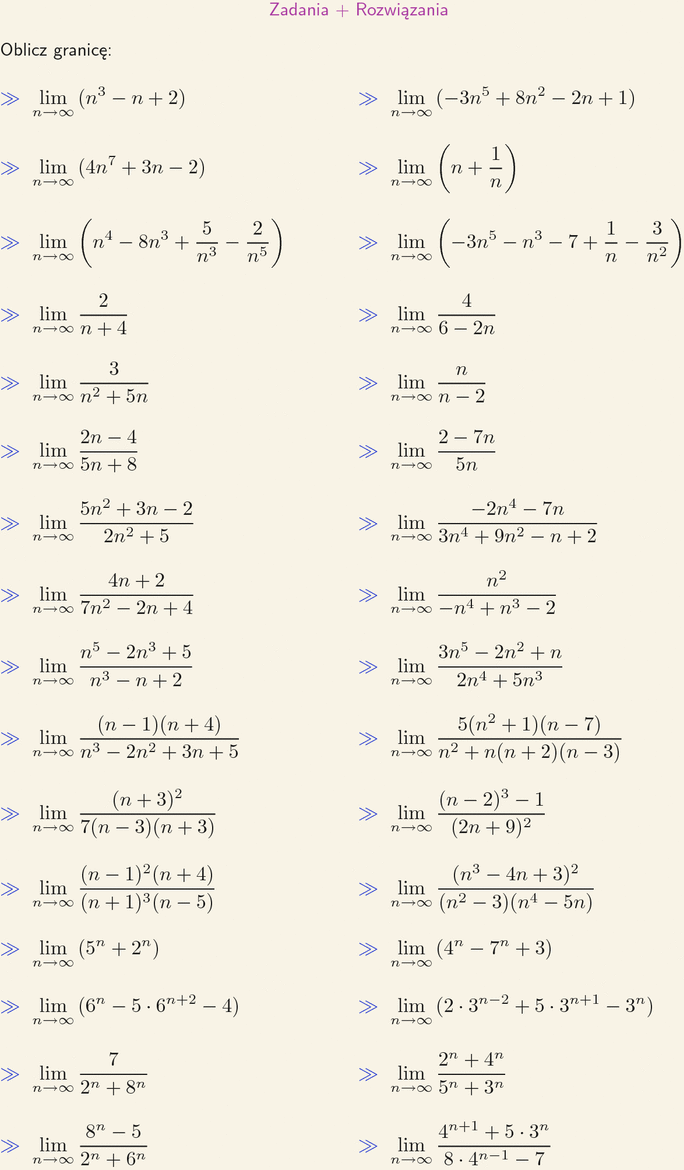
Zadania + Rozwiązania

Oblicz granicę:

lim (n^3 — n + 2) n—> oo	»
lim (4n‘ + 3n — 2) n—KX>	>
lim (n^Ą - 8n^3 + 4r - n—>oo \ nr n^b J	>
lim ^2 re->oo n + 4	>
lim —- n—>oo n~ + on	>
2n — 4 lim --- n—*oo on + 8	>
5n^2 + 3n — 2 lim ——;—-— n-*oo Zn* + 5	>
4n + 2 lim -—TT—--- n—Kx> In^2 — 2n + 4	>
n^5 — 2 n^3 + 5 lim —-- n—>oc n^ó — n + 2	>
Hm (»-!)(»+ 4) n—oo n^3 — 2n^2 + 3n + 5	>
^ i n—*oo 7(n — 3)(n + 3)	»
(n - l)^2(n + 4) n—oo (n + l)^3(n — 5)	>
lim (5"+2^n) n—*oo	>
lim (6" - 5 • 6^n+2 - 4) n—► oo	»
lim ^7 n-nx> 2^n + 8^n	»
8^n - 5 lim --— n—»oo 2^n + 6^n	>

lim (—3n⁵ + 8n² — 2n + 1)

1 _ _3_

n n²

n—>oo \    n

->oo 6 — 2n

n—*oo n — 2

..    2-7 n n—oo on

—2 n⁴ — 7 n

n—> oo 3n⁴ + 9n² — ra + 2

„2

n—oo —n⁴ + n³ — 2

3n⁵ - 2n² + n lim -:--—

n—»oo 2n⁴    5n**

5(„²+ !)(».-7) n—oo n² + n(n + 2)(n — 3)

lim ⁽r^2>:!:'

»—>oo (2 n + 9)²

(n³ — 4n + 3)²

n—oo (n² — 3)(n⁴ — 5n)

2"+4ⁿ lim ^-—

n—oo 5ⁿ + 3"

₄n+l ₊ 5.₃n

hm ——■—:-—

n—*oc 8 • 4” ⁴ — 7