image 057

Potencjały wektorowe i pola w strefie dalekiej 57

z

P(r’,e\(p-)

X

y

Rys. 3.1. Układ współrzędnych do analizy potencjałów wektorowych od skończonego rozkładu prądów elektrycznych lub magnetycznych

Należy podkreślić, że w większości praktycznych przypadków prądy, będące źródłami pola, mają charakter powierzchniowy lub liniowy, a w konsekwencji całkowania w (3.22) i (3.23) odbywają się po powierzchni lub wzdłuż konturu.

Rozważmy obecnie zachowanie się potencjałów w strefie dalekiej. Wprowadzając przykładowo do (3.22) warunki strefy dalekiej (2.24) i (2.25) uzyskujemy:

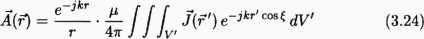
Zależność (3.24) wskazuje, że w strefie dalekiej, gdzie znajduje się nasz punkt obserwacji, następuje separacja pomiędzy zmienną r a pozostałymi zmiennymi, charakteryzującymi punkty źródeł i pola. Wprowadza to istotne uproszczenia przy obliczaniu pól w strefie dalekiej, gdyż w takiej sytuacji potencjał można zapisać w postaci:

(3.25)

A(r) = f(r) • [A!_r i_r + A'_ei₀ -f A'_v i<p]

gdzie f(r) = e^-jA:r/r, składowe zaś ze znakiem (') nie zależą od zmiennej r. Teraz obliczamy pola elektryczne i magnetyczne pochodzące od potencjału (3.25) wykorzystując kolejno związki (3.4) oraz (3.7) i (3.10). W tym celu będziemy musieli wykonać różniczkowania d/dr [/(r)], w wyniku czego uzyskamy składowe pól w postaci sum zawierających składniki proporcjonalne do czynników r^-n, gdzie n ^ 1. W przypadku strefy dalekiej, a więc dla r-4oo, pominiemy wszystkie składniki zawierające n ^ 2, gdyż będą one pomijalnie małe w stosunku do składników zawierających czynnik 1/r. W efekcie uzyskamy:

E_r ~ 0 Eg » —juAg

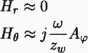
(3.26)

(3.27)