img058

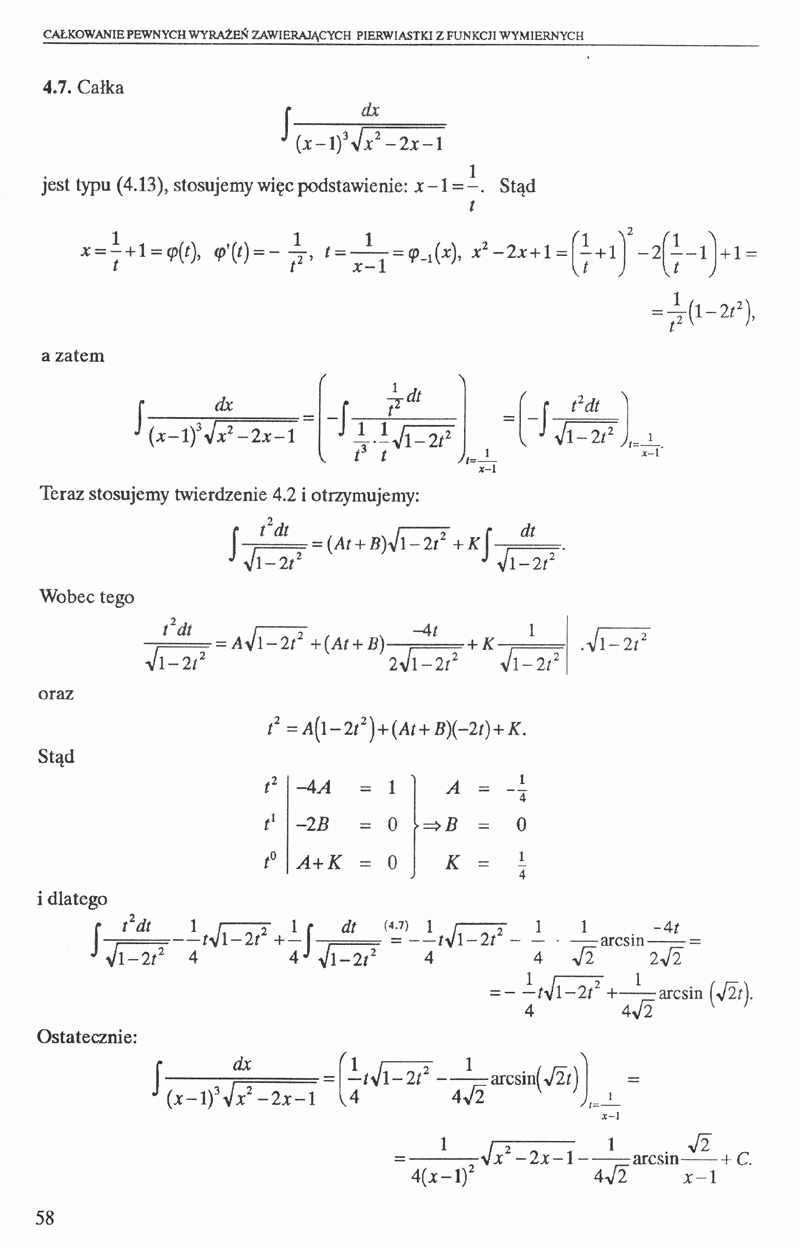
CAŁKOWANIE PEWNYCH WYRA?. EN ZAWIERAJĄCYCH PIERWIASTKI Z FUNKCJI WYMIERNYCH

4.7. Całka

J

dx

(x-\)³ylxⁱ-2x-l jest typu (4.13), stosujemy więc podstawienie: x-1 =-. Stąd

t

-* = y + ¹ = 9>(0>    ^< =    =    *²-2* + l=[j- + lj -2^y-lj + l =

a zatem

1

dx

■Jtt

^-Vl-2r² t³ t    ),

rdt

Vl-2/²

Teraz stosujemy twierdzenie 4.2 i otrzymujemy:

dr

2r

Wobec tego

r dr

Vl-2r^:

- = /tVl-2r² + (/tr + fl)

-4r    1

r+K-

2yl\-2t²    >/l-21²

.Vl-2r²

oraz

t² = zł(l-2r²)+(/tr + fl)(-2r)+/C

Stąd

-4/1    =    1

-25    =    0

/i+K = 0

i dlatego

J

a    4^J y]\-21²    4    ^

Vl-2r² 4

1    1    -4r

- • aresin-=

4    V2    2V2

=--rVl-2r² +—^—aresin (V2r).

4    4^2 ^{V 7}

Ostatecznie:

I

dx

(jt-1 )Vx² -2x-l

^ 1 .    j

—r VI-2r²--— arcsin( >/2r)

^4    4^2    ^{V ;}

X-l

+ C.

¹    n^-;—7    ¹    • ^

--vJt — 2jc — 1--—aresin-

58