img054

CAŁKOWANIE PEWNYCH WYRAŻEŃ ZAWIERAJĄCYCH PIERWIASTKI Z FUNKCJI WYMIERNYCH

1 1 1

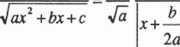
i w określonym przedziale (jakim?) całka (4.5) jest po prostu całką z ułamka prostego I. rodzaju.

Wobec tego, całkę postaci (4.5) (podobnie i całkę typu (4.4)) będziemy rozpatrywać jedynie w przypadku a * 0. Dodajmy jednak, iż jeśli a < 0, to z konieczności trzeba przyjąć, że A = b² - 4ac jest liczbą dodatnią, bowiem gdyby było a < 0 i A < 0, to funkcja podcałkowa zarówno we wzorze (4.4) jak i we wzorze (4.5) nie byłaby określona dla żadnego x e R.

Powyższe rozważania stanowią podstawę do sformułowania uwagi.

Uwaga 4.1

W dalszym ciągu całki typu (4.4) i (4.5) będziemy rozważać wyłącznie w następujących przypadkach:

1° a > 0 i A * 0,

2° a < 0 i A > 0.

Teraz możemy już zacząć obliczanie całki (4.5). W tym celu zauważmy najpierw, że

Wobec tego, na mocy już wcześniej uzasadnionych wzorów 20 i 18 zamieszczonych w tablicy 3 (strona 21), otrzymujemy

(4.6)

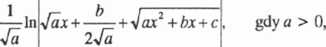
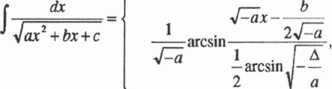
gdy a < 0

(zobacz uwagę 4.1).

Ale

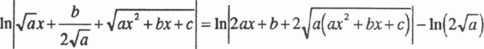
54