0037

(1)

(1)

39

§ 3. Całkowanie pewnych wyrażeń zawierających pierwiastki

Jako pierwszy przykład jej zastosowania rozpatrzymy całkę postaci

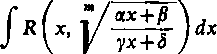
gdzie R oznacza funkcję wymierną dwóch argumentów, m — liczbę naturalną, a a, p, y, 5 są stałymi. Podstawmy

t = eo(x) =

= 9>( 0 =

_ OLX + P yx+b ’

x

dt^m-P

a—yt^m

Całka (1) przejdzie w całkę

j R (y(t), f)/(0 dt;

tu różniczka ma już postać wymierną, gdyż R, y, y' są funkcjami wymiernymi. Obliczywszy tę całkę według reguły poprzedniego paragrafu, powrócimy do starej zmiennej podstawiając z powrotem t = co (x).

Do całki (1) sprowadzają się także ogólniejsze całki

gdzie wszystkie wykładniki r, s,... są wymierne. Wystarczy tylko wszystkie te wykładniki sprowadzić do wspólnego mianownika m, by otrzymać pod znakiem całki funkcję wymierną zmiennej x i pierwiastka |/(ax+P)/(yx+S).

Przykłady.

y*+I+2

*>/■

(*+l)²- y/x+l

■ dx

Tutaj funkcja wymierna    sprowadziła się po prostu do funkcji liniowej. Przyjmijmy

_    yx+o

t = ]/x-i-l, dx= 2tdt, wówczas

f-A±l±2_-dx = 2    fU---f±². W

1 U+lp-^jt + l    J ‘ -1    J\»-l t¹ + t+\)

= ln ¹⁾²--^r-arctg-²'/¹' + C,

/^J+r+l ^3

2t+1

V*

pozostaje tylko podstawić jeszcze / = j/jc+l.

²>J-

dx

>/(x-l)(x+l)^J Przyjmujemy

-IV£f

dx

x+l

f³ + l ł³-l

dx = —

6t²dt

(»³-l)

2 ’