0041

43

§ 3. Całkowanie pewnych wyrażeń zawierających pierwiastki

które pozwalają zmniejszyć wykładnik p lub q o jedność, jeśli tylko suma p+q jest różna od —1.

Jeśli ani p, ani q, ani p+q. nie są liczbami całkowitymi, tak że całka J_p,_ą nie wyraża się w postaci skończonej przez funkcje elementarne, wzory redukcyjne można stosować wielokrotnie bez żadnych ograniczeń. Za ich pomocą można na przykład sprowadzić parametry p i q do ułamków właściwych.

Zatrzymamy się na ciekawszym dla nas przypadku, gdy całka może być obliczona w postaci skończonej. Można przy tym założyć, że wykładnik p lub q jest całkowity, gdyż przypadek, gdy p+q jest całkowite sprowadza się do przypadku całkowitego q przez podstawienie z = 1 /u.

Wtedy kilkakrotne kolejne zastosowanie wyprowadzonych wzorów pozwala sprowadzić wykładnik całkowity p lub q do 0, jeśli był on dodatni, lub do — 1, gdy był on ujemny. Na tym zwykle kończy się całkowanie lub w każdym razie znacznie upraszcza.

Przykłady.

1) Rozpatrzymy całkę (*)

H„ = f—    dx (m — całkowite) .

1 1 /u | 1 Tutaj n = 2, p = — -j-, dlatego gdy m jest nieparzyste, —-— = —^—jest liczbą całkowitą, a

gdy m jest parzyste, parzyste iest    Ą-p— — ^a więc w obu przypadkach można

n    2    2    2

obliczyć całki w postaci skończonej. Podstawienie z — x¹ sprowadza naszą całkę do postaci

|/(1 -z)-w*_z<»-n/_2<fe =y-_1/2.    .

Jeśli przy założeniu, że m>l, zastosujemy do tej całki wzór (IV), to otrzymujemy

m— 1 _T m

lub powracając do danej całki

tf.-—*■-¹ /T²

*^ł +

m-ł

m

H„-₂.

Zmniejszając mol wzór ten pozwala sprowadzić stopniowo obliczenie H_m albo do

H, = f ^xdx = -]/l-x¹ + C * }/l— x¹

dla m nieparzystego, albo do

H₀ = f -    = arc sin x+C

^J

dla m parzystego.

(') Analogicznie można też badać całki

I

X^m

l/x¹^l

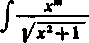
dx,

dx.

1

(1 -_z)i/y—o/»

2

m