img181

Dodatek 1

Problem wyboru metryki w przestrzeni cech

Definiując w rozdziale 4 metody minimalnoodległościowe bazowano na istnieniu w przestrzeni cech X metryki p, której charakter nie był bliżej omawiany (por. wzór (22)). Obecnie zajmiemy się przydatnością konkretnych metryk. Najbardziej naturalna wydaje się zawsze metryka Euklidesowa, definiowana wzorem:

\

v = \

(Dli)

Metryka ta odpowiada obiegowej definicji odległości i z tego powodu jest chętnie, odruchowo wręcz, stosowana w wielu praktycznie realizowanych algorytmach. Należy zdawać sobie sprawę, że metryka ta ma wiele wad. Wskazując niektóre z tych wad, możemy zaproponować inne warianty metryk.

Pierwsza wada wynika z ewentualnych różnic wymiarów poszczególnych składowych wektora x. Jeśli składowa x wyraża się - przykładowo -wartością rzędu 10⁶, a pozostałe składowe - wartością rzędu 10“⁶, to oczywiście wzór (Dl.l) uzależnia odległość p\ wyłącznie od wartości składowej x_v przy całkowitym ignorowaniu pozostałych składowych. Najczęściej efekt taki jest całkowicie niezgodny z zamierzeniem twórcy metody, gdyż podważa celowość pomiaru pozostałych cech i niweluje wnoszoną przez nie informację. Jedyne rozsądne rozwiązanie polega wówczas na zastosowaniu mnożników normalizujących i uogólnionej metryki Euklidesowej o postaci:

P2 ) ¥? )

*!)]*■

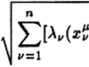
(D1.2)

Mnożniki normalizujące A mogą być w różny sposób związane z wartościami składowych wektora x_v. Przykładowo możną opierać je na przedziale zmienności

(Dl .3)

\ -___

A._v —    .    1

max Xfnt mm x£U    z£U