3818438382

Przestrzenie Metryczne

Definicja

Niech X -zbór,

Metryką (odległością) wzbierze X nazywamy funkcję d :

(MO) d: XXX -»[0, -f oo)    (nieujemność)

o własnościach:

(M1) VxjeX:    d(x,y)—0 <*>x=y

(M2)    d(x, y)=d(y,x)    (symetria)

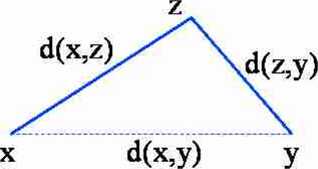
(M3) Vx,y,z^X: d{x,y)<d(x,z)+d(z, y)    (warunek trójkąta)

Parę (X,d) nazywamy przestrzenią metryczną.

Uwaga

(M1)<=»[Vx^X d(x, x)=0 A(Vx, d(x, j>)=0    j>)]

Przykłady przestrzeni metrycznych

1) Przestrzeń dyskretna

Vx, yeX: d_0l{x, y):= \

(X,dJ

0,    gdyx—y

1,    gdyx*y

do, - metryka dyskretna (zero-jedynkowa)

Sprawdzamy, że funkcja d_m jest metryką, tzn. Jest dobrze określona i spełnia warunki (M0)-(M3).

Dowód

(MO)-(M2) wynikają z definicji d_0l (M3)

pi*‘^yhD}    ^

2. x^y L=d(x, y)= 1

x=z¥=y P — d{x,z)+d{z,y)= Q-fl=l y=z¥=x    P = d(x, z)+d(z, y )= 1+0=1

y^z^x P = d(x, z)+d(z, y)= 1 4-1 =2 -

=>P>1

^>L<P

□

Wykład dr Joanny Górskiej    strona 1 z 23    Opracowali: Robert Paka, Michał Pawłowski