img191

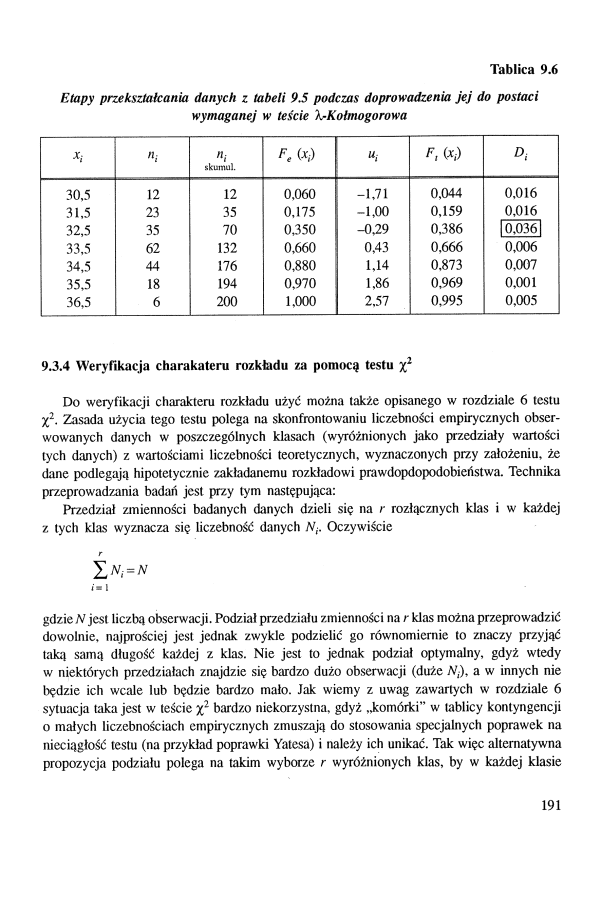
Tablica 9.6

Etapy przekształcania danych z tabeli 9.5 podczas doprowadzenia jej do postaci wymaganej w teście hrKołmogorowa

	^ni	^n, skumul.	F* W	ut	f, w
30,5	12	12	0,060	-1,71	0,044	0,016
31.5	23	35	0,175	-1,00	0,159	0,016
32,5	35	70	0350	-0.29	0.386	[00361
33,5	62	132	0,660	0,43	0,666	0,006
34,5	44	176	0,880	1.14	0,873	0,007
35,5	18	194	0,970	1,86	0,969	0,001
36,5	6	200	1.000	2,57	0,995	0,005

9.3.4 Weryfikacja charakatcru rozkładu za pomoc? testu x²

Do weryfikacji charakteru rozkładu użyć można także opisanego w rozdziale 6 testu X². Zasada użycia tego testu polega na skonfrontowaniu liczebności empirycznych obserwowanych danych w poszczególnych klasach (wyróżnionych jako przedziały wartości tych danych) z wartościami liczebności teoretycznych, wyznaczonych przy założeniu, że dane podlegaj? hipotetycznie zakładanemu rozkładowi prawdopdopodobieństwa. Technika przeprowadzania badań jest przy tym następująca:

Przedział zmienności badanych danych dzieli się na r rozłącznych klas i w każdej z tych klas wyznacza się liczebność danych N,. Oczywiście

r

I Ni = N

im 1

gdzie N jest liczbą obserwacji. Podział przedziału zmienności na r klas można przeprowadzić dowolnie, najprościej jest jednak zwykle podzielić go równomiernie to znaczy przyjąć taką samą długość każdej z klas. Nie jest to jednak podział optymalny, gdyż wtedy w niektórych przedziałach znajdzie się bardzo dużo obserwacji (duże A',), a w innych nie będzie ich wcale lub będzie bardzo mało. Jak wiemy z uwag zawartych w rozdziale 6 sytuacja taka jest w teście x² bardzo niekorzystna, gdyż „komórki” w tablicy kontyngencji o małych liczebnościach empirycznych zmuszają do stosowania specjalnych poprawek na nieciągłość testu (na przykład poprawki Yatesa) i należy ich unikać. Tak więc alternatywna propozycja podziału polega na takim wyborze r wyróżnionych klas, by w każdej klasie

191