kolo bartol III 01 02 by kar

ANALIZA MATEMATYCZNA, 2001/2002, KOLOKWIUM III, 20 marca 2002

1.    Znaleźć równanie stycznej do wykresu funkcji f(x) = w jej punkcie przegięcia.

2.    Wykazać, że dla każdego x 6 (0, |) zachodzi nierówność

tg(^) >x +

3.    Rysunek przedstawia wykres funkcji /', pochodnej pewnej funkcji /. Wskazać przedziały rnonotonicznośei i ekstrema lokalne funkcji / oraz przedziały jej wypukłości i wklęsłości.

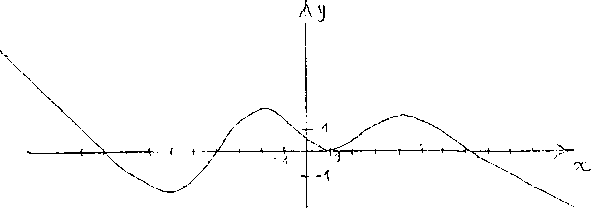
4.    Wykazać, że gdy 0 < 0 < a < §, to < tg a - tg 0 <

5.    Wykazać, że e + 2e² + 3e³ + ... + 99e" > (1 -1-2 -h 3 -!- ... + 99)c⁵⁰.