kolo bartol IV 02 03 by kar

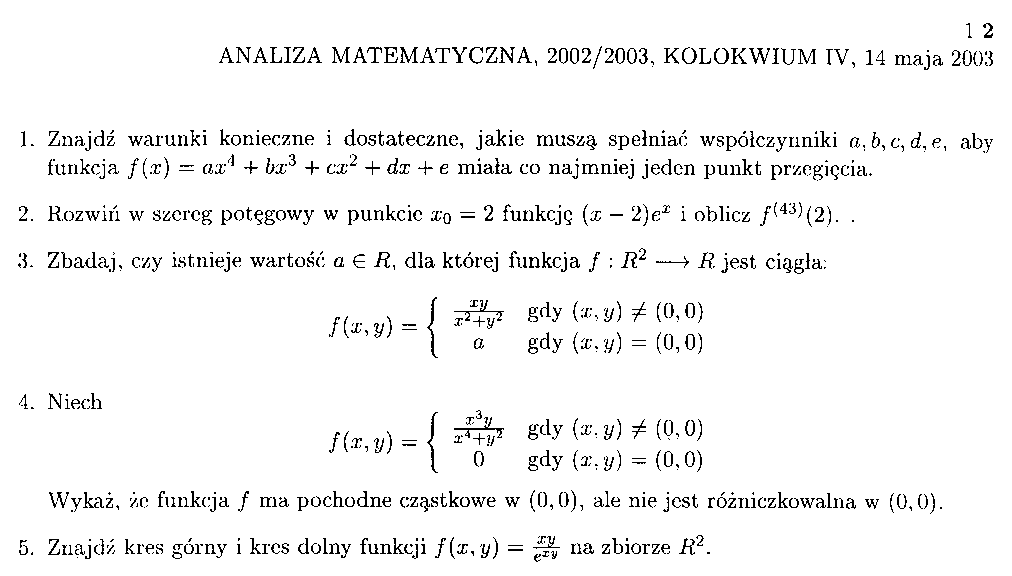
ANALIZA MATEMATYCZNA, 2002/2003, KOLOKWIUM IV, 14 maja 2003

1.    Znajdź warunki konieczne i dostateczne, jakie muszą spełniać współczynniki a, t>, c, de, aby funkcja f(x) — ax^ri + Ac³ + cx² + dx + e miała co najmniej jeden punkt przegięcia.

2.    Rozwiń w szereg potęgowy w punkcie = 2 funkcję (x - 2)e^x i oblicz /(⁴³)(2). .

3.    Zbadaj, czy istnieje wartość a € R, dla której funkcja / : R² —> R jest ciągła:

fi^y)

f ^ g(iy (*,y) ^ (0,0)

\ a gdy (x.y) = (0,0)

4. Niech

f(x,y)

^ gdy (x,y) / (0,0) 0 gdy (a\y) = (0,0)

Wykaż, że funkcja / ma pochodne cząstkowe w (0,0), ale nie jest różniczkowalna w (0,0).

5. Znajdź kres górny i kres dolny funkcji f{z, y) — /// na zbiorze R².