kolo bartol I 01 02 by kar

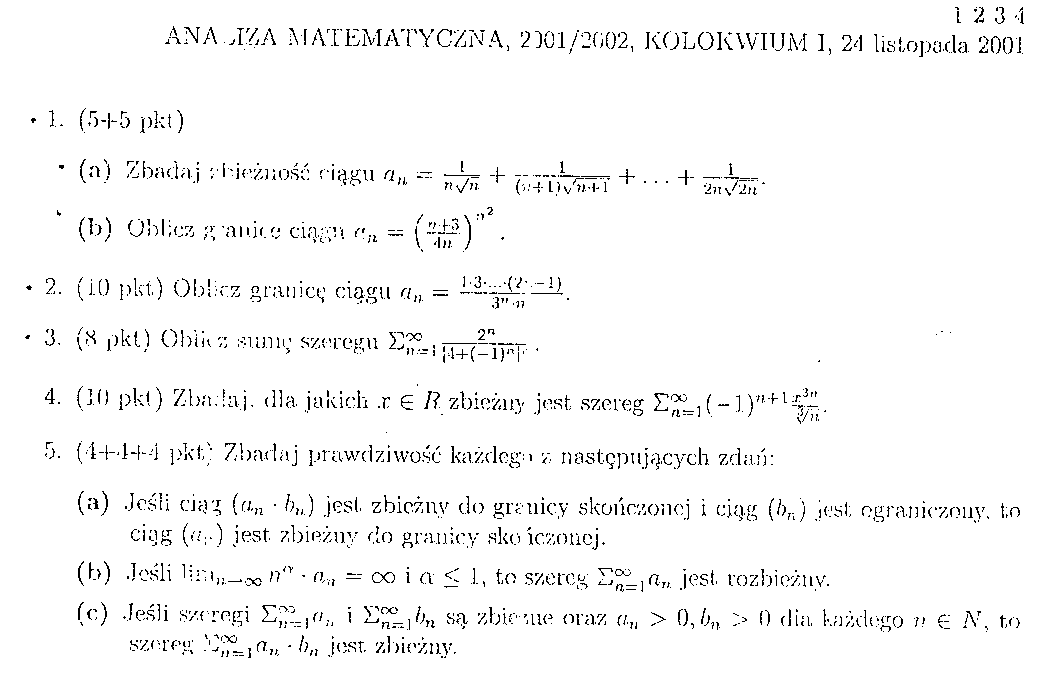
i 2 3 4

ANALIZA MATEMATYCZNA, 2DO 1/2002, KOLOKWIUM 1, 24 listopada 2001

1- (0-05 pkt)

’ (n) Zbadaj r i-jeżu oś:

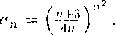
(b) Oblicz g anice cm.

2.    (10 pkt) Oblicz gran i a; ciągu a„ — ~'~'g7ry"—~ ■

3.    (3 pkt) Obi im,; sumę szeregu S3°., rr-j-—- ,

4. (II) pkt) Zbadaj, dla. jaki eh .cOf zbieżni/ j ust szereg £ jjb ₁ ( — 1) ⁺¹ ^.

5.    (4-04-04 pkt; Zbadaj prawdziwość każdego z następujących zdań:

(a)    ■Jeśli ciąg (a._n ■ />„.) jest zbieżny do greuicy skończonej i ciąg (b_n) yret ograniczony, to ciąg (ey) jest zbieżny do granicy sko iezonej.

(b)    .Jeśli    n'^T ■ n„ — oo i a < .1, to szereg Iy=,ry jest. rozbieżny.

(c)    Jeśli szeregi Ejjlpy i EJi, h_n są zbiezue oraz ry > 0 ,b_n > 0 di a, każrlego v fi N, to szereg rejd] o,, - /)„ josT. zliicżny.