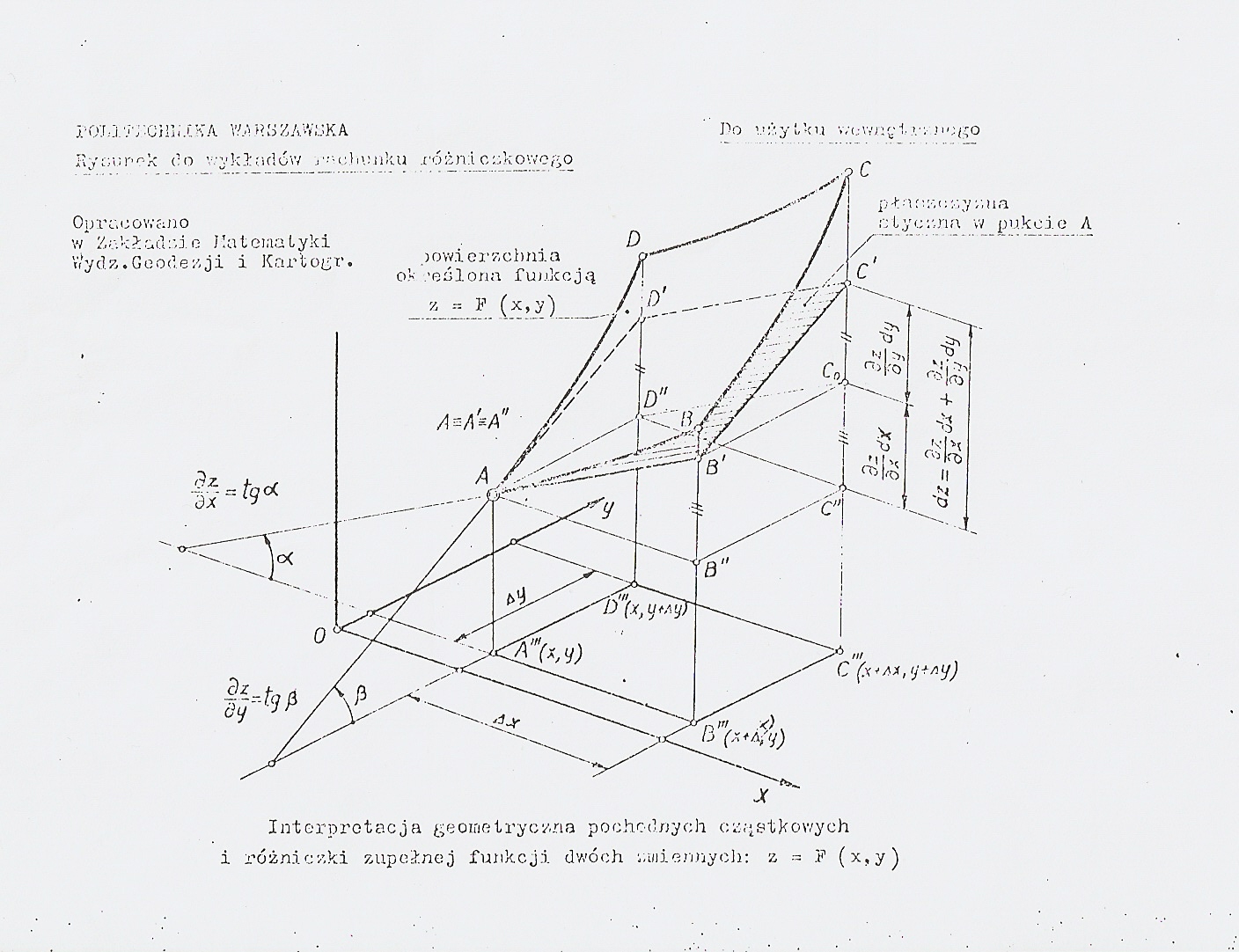
interpretacja geometryczna pochodnych czastkowych
POLIittCHli.CKA WARSZAWSKA Do użytku v/o\vnę1,?.B}i<;go
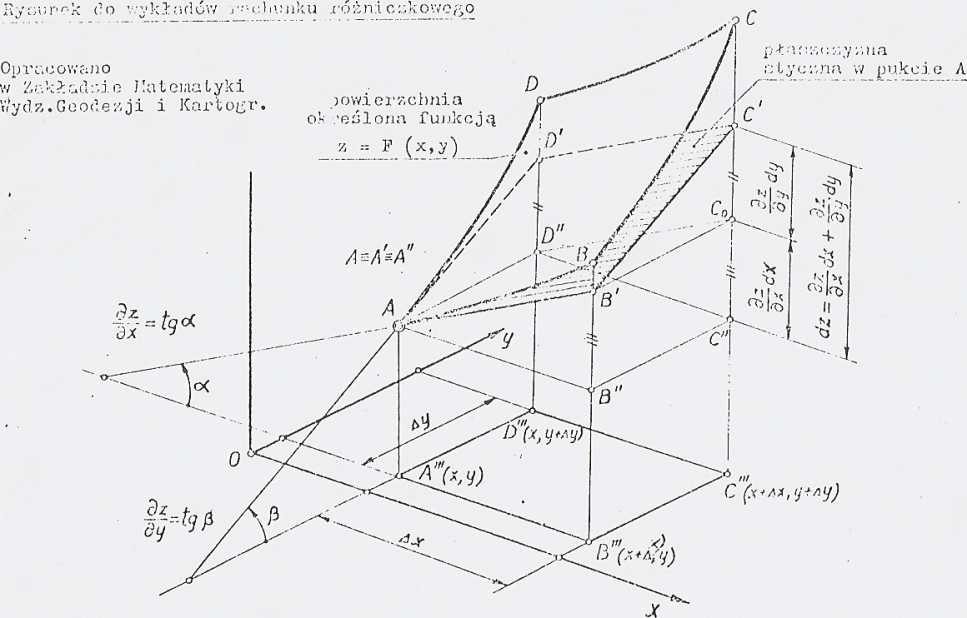
Interpretacja geometryczna pochodnych cząstkowych i różniczki zupełnej funkcji dwóch zmiennych: z = ? (x,y)
Wyszukiwarka
Podobne podstrony:
zdjecie0008 7 V. Interpretacja geometryczna pochodnych cząstkowych w przypadku n - 2................
034 8 Interpretacja geometryczna pochodnej Załóżmy, że funkcja / ma w punkcie xq pochodną,. Wówczas
Twierdzenie 6.8 (Taylora) Jeżeli funkcja f ma ciągle pochodne cząstkowe do drugiego rzędu włącznie n
293 (8) W 01 11.2.1. Pojęcie pochodnej funkcji w punkcie (III) Interpretacja geometryczna pochodnej
Definicja funkcji wielu zmiennych. Dziedzina funkcji wielu zmiennych i jej interpretacja geometryczn
37380 img455 (2) Czy zauważasz różnicę?Interpretacja geometryczna pochodnej funkcji w punkcie Zastan
h08 Bogatko Herb Pomian horbji Pomian. Stary polski ród Bogatków pochodzi z ziemi czerskiej, spod Wa
img099 99 ma pierwsze pochodne cząstkowe w punkcie a i a Jest punktem ekstremum lokalnego, to Warune
img070 70 (j - 1, n) (6.5) Wzory (6.4) i (6.5) noszę nazwę reguły wyznaczania pochodnych cząstkowych
img094 94 aa pierwsze pochodne cząstkowe ograniczone « I. Ponadto zakładamy, że a21 pochodna
img099 99 ma pierwsze pochodne cząstkowe w punkcie a i a Jest punktem ekstremum lokalnego, to Warune
img099 99 ma pierwsze pochodne cząstkowe w punkcie a i a Jest punktem ekstremum lokalnego, to Warune
gdzie fa - wektor wierszowy zawierający pochodne cząstkowe
więcej podobnych podstron