RP2

2

10.    Sprawdzić, że ciąg a„ = 1/n - 1/ n+1 określa rozkład prawdopodobieństwa zmiennej losowej

X, która przyjmuje wartości n = 1,2,3..... Obliczyć P(X < 3), P(X < 2).

11.    Czy funkcja F(x) = 1 /1 + X² może być dystrybuantą zmiennej losowej typu ciągłego dla:

a) -oo<x<a>; b) 0 < x < oo ; c)- oo< x < 0 .

12.    Dana jest funkcja gęstości:

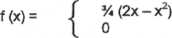
dla 0<x<2 dla pozostałych x

Znaleźć dystrybuantę zmiennej losowej X i obliczyć P(X < 1).

13. Dystrybuanta zmiennej losowej X ma postać:

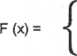
0

A + B • arcsin x/a 1

dla x<-a dla | x | < a dla x s a

a)    dla jakich A i B zmienna X jest zmienną losową ciągłą ?

b)    znaleźć gęstość zmiennej losowej X.

14. Gęstość zmiennej losowej X ma postać:

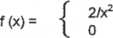
dla | x | > a dla l x I s a

a) wyznaczyć stałą a ; b) znaleźć i narysować dystrybuantę F(x); c) obliczyć i zaznaczyć na wykresach gęstości i dystrybuanty P( IXI > 5); d) wyznaczyć xo takie, że P( X ł xo) = 1/8; e) znaleźć rozkład zmiennej losowej Y = e^x .

15. Gęstość zmiennej losowej X ma postać:

dla x>0

dla pozostałych x

Wyznaczyć gęstość prawdopodobieństwa zmiennej losowej: a) Y = e*; b) Z = 1/ X². 16. Zmienna losowa X ma gęstość określona wzorem:

Znaleźć gęstość prawdopodobieństwa zmiennej losowej Y = e'^x .