metody11

110

sowymi, mającymi określony rozkład prawdopodobieństwa. Rozkład, ten zależy od rozkładu zmiennej w całej populacji i od wielkości próby. Na ogół wyróżnia się dwa rodzaje rozkładów statystyk. Są tot

-    rozkłady dokładne (zMfifŚ czasami rozkładami z małej próby),

-    rozkłady asymptomatyczne (zwane rozkładami granicznymi).

Rozkładem dokładnym Jakiegoś parametru wyliczonego dla próby składającej się z n elementów jest rozkład prawdziwy dla wszystkich liczb naturalnych n« Jest to zatem rozkład zależny od n, ale niezależny od wielkości próby.

Rozkładem asymptomatycznym jest taki rozkład, do którego dąży rozkład dokładny tego parametru z próby, przy założeniu, że n zdąża do nieskończoności,

6.1.1. Rozkład średniej aryimełycznej z próby

Jeżeli ze zbiorowości generalnej o rozkładzie X: N(X; s(x)) pobierzemy losowo w sposób niezależny szereg prób składających się z n elementów, to zmienna losowa x (czyli średnia arytmetyczna dla próby) ma również rozkład normalny wyznaczony parametrami X;

TH

że "dokładnym rozkła-

Można zatem powiedzieó,

czyli 5: n(x;

dem średnich z prób n-elementowych pobranych w sposób niezależny z populacji o rozkładzie normalnym o znanej średniej i odchyleniu standardowym jest także rozkład normalny, którego średnia jest równa średniej populacji generalnej, a odchylenie standardowe wynosi

Ml) J

Z twierdzenia tego (zwanego także centralnym twierdzeniem granicznym) wynika przede wszystkim spostrzeżenie, że wraz ze wzrostem liczebności próby maleje odchylenie standardowe rozkładu średniej z próby. Im zatem mniejsze n, tym mniej szpiczasty rozkład (rys. 6,29.)

M, Krzysztofiak, A. Luszniewiczj Statystyka. Warszawa 1979, s. 132,

Rys. 6.29. Rozkład- z próby i rozkład populacji generalnej

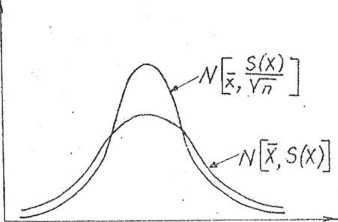
Zauważmy także bez udowadniania, że gdy procedurą taką zastosujemy w odniesieniu do populacji generalnej o rozkładzie asymetrycznym, to rozkład średnich z prób będzie rozkładem normalnym przy założeniu, że wylosowane próby będą spełniały warunek n ^30. W ten właśnie sposób realizuje się tzw. prawo wielkich liczb, mówiące o tyra, że przy losowym pobieraniu prób n-elementowych ze zbiorowości o dowolnym rozkładzie wyznaczonym średnią arytmetyczną i odchyleniem standardowym wzrost n sprawia, iż rozkład średniej z próby zmierza do rozkładu normalnego. Jak więc widaó, prawo wielkich liczb ma istotne znaczenie praktyczne, ponieważ pozwala na pomijanie założenia o normalności rozkładu populacji generalnej.

Ważne znaczenie praktyczne ma także tzw, rozkład różnicy dwóch średnich arytmetycznych z próby, wyznaczony dla niezależnie    pobra

nych prób ze zbiorowości o rozkładzie normalnym. Jeżeli X:N(X; S(x)) i Y: N(Y{ S(.Y)) przy założeniu, że X i Y są niezależne, to zmienna losowa V = X - Y jest także zmienną losową -

V:

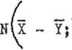
s²(x)    s²(Y)

n    n

6.1.2. Rozkład Słudenfa

Omawiany rozkład średniej w próbach pobranych zej zbiórowosoi o rozkładzie normalnym uzależniony był między innymi od odchylenia standardowego tej zbiorowości. Z reguły jednak parametr ten nie jest