Lista 3

LISTA 3

•' 1.',Manny dany rozkład prawdopodobieństwa zmiennej losowej X.

V^(X = I'j) = o;i P(X = 0) = 0,3 P(X = 2) ~ 0,2 :P(vY —3) = 0,4

Wariancja zmiennej losowej X wynosi:

A) 2,25 B) 1    Ć) 1,5    D) 4,5    E) żadna z powyższych

\(y)=%y_i -fii i -Ą-ąi + o-ąi+Z'ąz4 z.qk- A,y

f.    ■ .    *    .    .    ..

V którym z niżej wymienionych rozkładów wartość oczekiwana jest zawsze wiesza od wariangi? Poissona    U) normalny    III) dwumianowy (BemoufiPego)

A) tylko Ii II

D) LII i III

B) tylko I! i HI C) tylko M

E) żaden z powyższych wariantów

^Wiadomo, że wpartii żarówek jest 1% braków. Wylosowano niezależnie do próby 240 żarówek Jakie jest prawdopodobieństwo, że będą wśród nich co najmniej 2 braki?

1,308

B) 0,570

C) 0,692

D) 0,430

E) żadna z powyższych

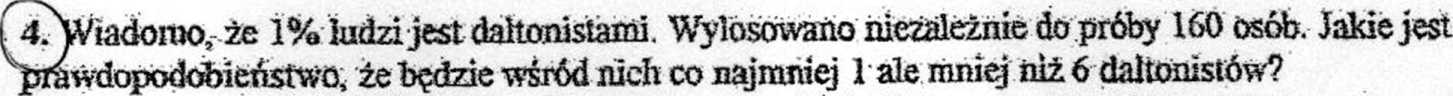
A) 0,469

B) 0,797

C) 0,792

D) 0,474

E) żadna z powyższych

yCWskaż warunki, przy których stosuje się pokład BemouUi’ego dla losowania kul z urny.

iń) próby są niezależne kule mogą się powtarzać    Ty)kule nie mogą się powtarzać

A) tylko 11 i ID C> tylko U i IV

B) tylko I i m

D) tylko I i IV    E) żaden z pow. wariantów

_adopgjff

^    (prawdopodobreństwo wystąpienia chłopca jest takie samo jak dziewczynki).    j)D.I) ~ ^

^3, k.-o - p^ręi    .

A)-    B)-    jtojt-    D)~

⁷ 8    8    ^8    3

'3 o

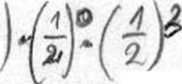
E) żadna z powyższych C £    ^

C C J/C— ^

C 3>I>s-

o) --

Szansa na udany "strzał” w teście ze statystyki wynosi 1/5. Nieprzygotowany student oddal 15 strzałów. Jakie

:t prawdopodobieństwo, że nie odpowie poprawnie na żadne pytanie?

15    lis

c:po£- _v

T> C P<ł- Y

3

- C) -

5 _v    4

<,ys

a- ^A    -¹!

r = IV?

E) żadna z powyższych ^    | ^

4    B) i—    U) —    U) i-

8. W urnie mamy 4 kule białe i 6 knl czarnych. Losujemy ze zwracaniem trzy kule. Jakie jest prawdopodobieństwo, że wylosujemy dokładnie dwie kule białe

D) i

A)

\

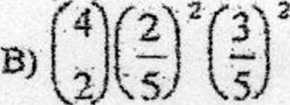
JW-

W

V57 V5.

\s

IJ

i YjiY

Ad) \ao|

3V £\ Ys}¹

2JI10J llO;

E) żadna 7. powyższych

f (y-2) =