Statystyka5

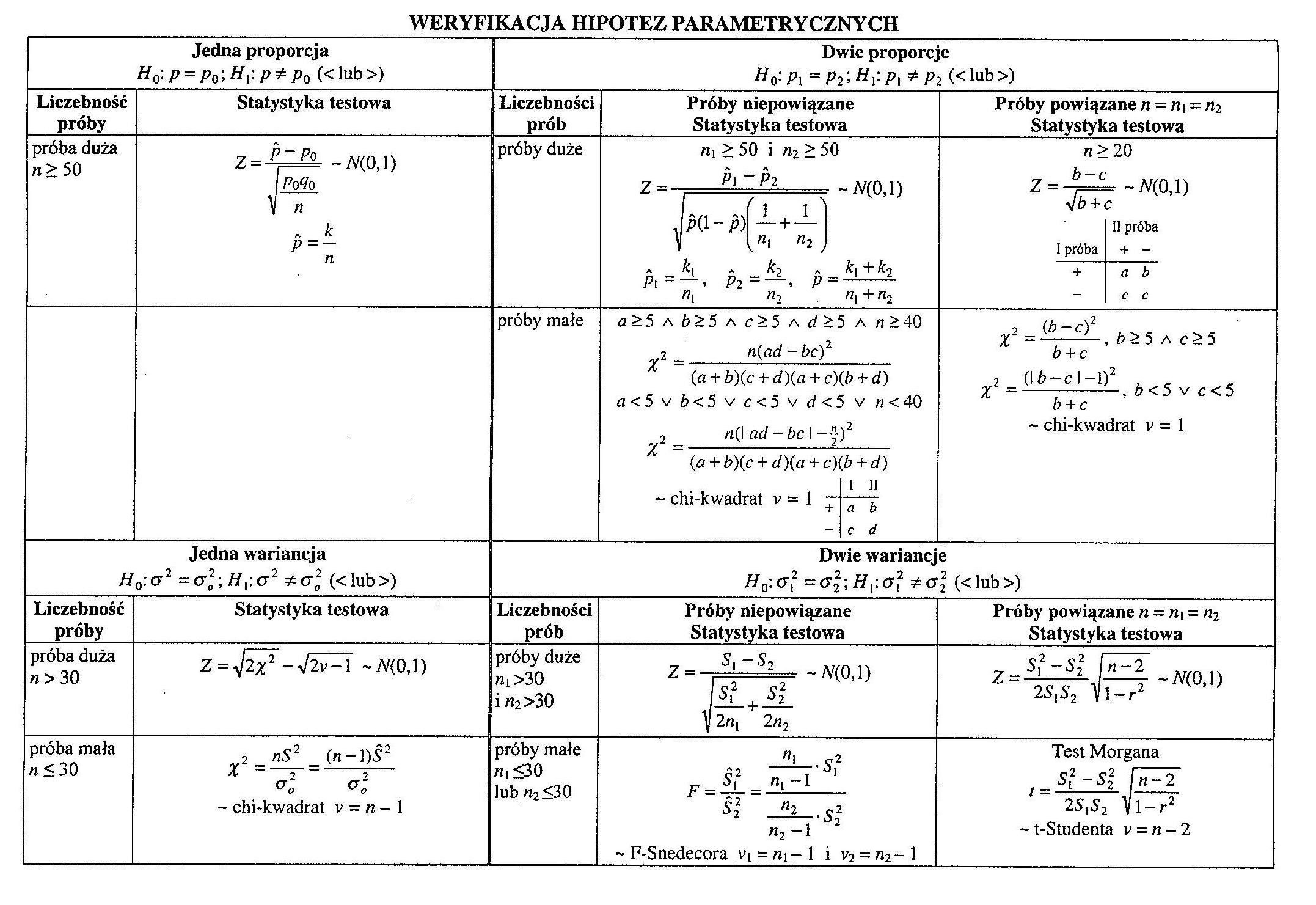
WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH

Jedna proporcja

P = P0’^H\^: P* Po (<lub >)

Dwie proporcje

H₀: p_x =p₂\Hp_x * p₂ (< lub>)

Liczebność

próby

próba duża n> 50

Statystyka testowa

Z=P—M ~N(0,1)

Po%

* k

P = ~

n

Liczebności

prób

próby duże

z =

Próby niepowiązane Statystyka testowa

n\ > 50 i n₂ > 50

A    A

Pl-P2

m-P)

^r\ 1 ' —+— n_{ n₂

0,1)

Próby powiązane n = n_x-n₂ Statystyka testowa

Pi

*    £1 + k₂

P = ~-~

n_{ + n₂

próby małe

a> 5 a fe>5 a c>5 a d >5 a n> 40

z² —

n(ad -bc)‘

n> 20

=4=ł -m. i) yjb +C
	II próba
I próba	+ —
+	a b
-	c c
0-c)^2b + c	b > 5 a c > 5

(a + b)(c + d){a + c){b + d) a <5 v b <5 v c <5 v d <5 v n< 40

_t2

z² =

n(ł ad -bc I

(« + b){c + d)(a + c)(b + d) 1 II

- chi-kwadrat v = 1

a b c d

X

₂    (\b-c\-\y

,b<5v c < 5

6-f c

chi-kwadrat v = 1

Jedna wariancja

H₀:<J² ~ c²; H<r² *cr² (< lub >)

Dwie wariancje

H_q: o? - g\ ; H{. o? * g\ (< lub >)

Liczebność próby	Statystyka testowa	Liczebności prób	Próby niepowiązane Statystyka testowa		Próby powiązane n « nt = n2 Statystyka testowa
próba duża n > 30	Z = '/2?"-V2v-l ~AT(0,1)	próby duże n 1 >30 i n2 >30	z -	^S1 52 ~ w(n i)	5,^2 - 52^2 1 n - 2
				C2 n2 ’ j	^Z- 2StS2 i-V ~^mi)
			1	2nx 2n2
próba mała n < 30	,.2 «S^2 (n-l)Ś^2	próby małe ni <30 lub n2<30		n2	Test Morgana
	X 1 2 - chi-kwadrat v = rc - 1		f_Ś? _ nx-l śś ”^2 .Si n2 -1 ~ F-Snedecora vi = «i- 1 i v2- n2~ 1		s_S}-Si In-2 2S,S2 V 1-r^2- t-Studenta v = n - 2