Strona0244

244

Przez podstawienie siły tarcia T wyrażonej wzorem (10.9) do (10.10) otrzymamy

244

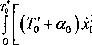
d< = 0

(10.11)

Ponieważ pochodna x zgodnie z (10.8) i_t = A<d_q cos , więc

^J0

J ('T' + a₀)cos²G)_Qt

—T£ A a>_Q cos³ a)₀t +i TqA²(oI cos⁴ a>₀t 2 6

dć-0(10.12)

Po scałkowaniu równania (10.12) otrzymamy amplitudę drgań samowzbudnych w postaci:

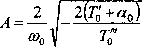
Ponieważ suma (7J + a_o)<0, więc wyrażenie pod pierwiastkiem jest dodatnie tylko przy 7^ > 0 . Często można pominąć wszystkie niesprężyste opory oprócz siły tarcia T. Przez podstawienie ccq = 0 otrzymamy bardzo prostą zależność na amplitudę drgań

A

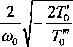
(10.13)

Wyznaczamy amplitudę drgań samowzbudnych dla przypadku, gdy charakterystyka tarcia (rys. 10.5) jest opisana równaniem

T = 3T

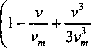
(10.14)

gdzie: T_m, v_m - odpowiednio siła tarcia, prędkość względna w punkcie minimum charakterystyki.

Nominalna prędkość ślizgania v₀ znajduje się na opadającej części charakterystyki w pobliżu minimum v i wynosi 0,95 v_m. Przez różniczkowanie równania

(10.14) otrzymamy:

r

371

-V-H

3