WM008

Uwzględniając zależność [9-2] otrzymamy

= 0;

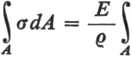
zdA = 0.

[9-3]

Ponieważ — ^ 0, rozpatrujemy bowiem wygięty element belki o promieniu q J= oo, więc musi być $ zdA = 0. Stąd wynika, że moment statyczny przekroju

A

poprzecznego belki względem osi obojętnej S_y = J zdA = 0, a zatem oś obojętna

A

przechodzi przez środek ciężkości przekroju, który leży na osi symetrii z. Punkt 0 pokrywa się ze środkiem ciężkości C przekroju, a więc oś x jest osią geometryczną rozpatrywanej belki (lub pręta).

Dalej mamy

= 0;    ^oydA

A

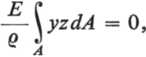
[9-4]

a zatem musi być J yzdA = 0.

A

Ponieważ całka ta wyraża wartość momentu odśrodkowego J_yz, a zatem osie y i z są głównymi środkowymi osiami bezwładności przekroju poprzecznego belki. Warunek [9-4] jest spełniony dla każdego przekroju symetrycznego względem płaszczyzny sił. Jeżeli przekrój poprzeczny belki nie ma żadnej osi symetrii, wówczas warunek J_zy = 0 będzie spełniony, gdy płaszczyzna działania momentu przechodzi przez oś belki oraz jedną z głównych osi bezwładności przekroju.

Wreszcie równanie ostatnie daje

Y.M_y = 0; M_a- J ozdA = 0,    [9-5]

A

a więc

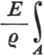
z²dA = M_a.

Ponieważ jj z²dA wyraża moment bezwładności J_y przekroju poprzecznego belki

A

względem osi obojętnej, więc otrzymamy

[9-6]

1 M_a

q EJ_y

Ze wzoru tego wynika, że im większy jest — przy danej wartości momentu zginającego M_a — moment bezwładności przekroju belki J_y, tym większy będzie promień krzywizny q, a więc mniejsze ugięcie belki.