zdjecie0026

28

Stąd i z równości (1.5) wynika, Ze lin -\/"T -    1.

n—

b) jcicli 0 < A < 1, to B - j jest liczbą większą od jedności. Z pierwszej części dowodu otrzymajeoy

lin \/^rT -    1.

a—-cc

A - lin ■P/J - li® ^ ,_.

n—so V    n_Kp

1

Z drugiej otrony lin -^a

n—-co co kończy dowód.

2. a -

. Poalewai a i, więc

tyⁿ>¹ —ⁿ~ “ ¹ ♦ ^dn» d_a> O.

Udowo dniny, Ze lin

n-»«j

(1.8)

Zate®

5(5) C •    *„²-

S tąd, dla n > 1

srfrfr-

2 nierówności (1.9) na podstawie twierdzenia o trzech ciągach otrzymujemy

lin

a-woo

d

n

O .

Stąd i z (1.8) wynika, Ze

li® n—**>

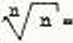
1 .