0000115

■sinych ( n te] sieci. Łuki <x,y> , takie że x tAoyeO ^ł(x,y) »1 okreóloję zbiór krowędzi U^łC U tworzący skojarzenie najliczniejsza grafu C.

Za względu na ezczególnę postać tworzonej elecl S (prze -pustowoóć równa 1 lub co i dwudzlolność grafu C). algoryta wyznaczania przopływu maksymalnego można znacznie uprościć. Uproszczony algorytm nooi historyczno nazwę algorytmu wyznaczania najliczniejszego zbioru niezależnych oczek dopuszczalnych. Nazwa •oczko dopuszczalno" bierze się etfd, że grof C przedstawia elę w postaci prootokętnej tablicy, w której wiersza odpowladaję eleaentoa zbioru A, kolumny - elementom zbioru 0, a kratki nie przokreólono (oczka dopuszczalne) odpowiadajo krawędzloa gro -fu G. Pozoetoło oczka.tej tablicy przekreśla się..

Na przykład grof G z rys.14.3 Jest przodstowiony w postaci tablicy Jak na rys.1.47.

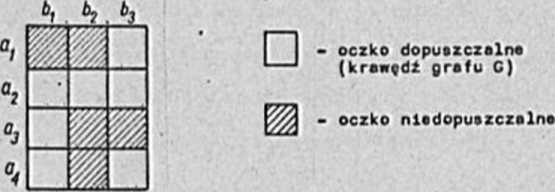
Rys.14.7

Wybrany zbiór oczek dopuszczalnych będzie stanowił zbiór oczek niezależnych, gdy w każdym wierszu 1 w każdoj kolumnie, omawianej tablicy, będzie wybrane nie więcej niż Jedno oczko (każde dwie gałęzie skojarzenia muszę być nleprżyległe).

W oploonym niżej algorytmie, wybierane oczka oznacza elę jedynkami.

Algorytm wyznaczanie najliczniejszego zbioru niezależnych oczek dopuszczalnych

0 a n a t Tablica możliwości przydziału (graf C) Procedura :

W tablicy znajdujemy dowolna, dopuszczalna rozmieszczenia jedynak w oczkach dopuszczalnych.

Cachujomy kreskę wezyetkie wiersze tablicy bez Jedynak. Wiersze te staję cię ocechowane i niesprawdzone.

Py*emy, czy zbiór ocechowanych i niesprawdzonych wierszy Jeet puoty? Oożoli tak, to przechodzimy do (5⁰) . w prze -ciwnym przypadku, dla każdego ocechowonogo 1 niesprawdzo -nogo wiereza, cechujemy, numerem tego wioraza, nieocecho -wane do tej pory kolumny tablicy, odpowiadajęco oczkom dopuszczalnym w tym wierszu. Kolumny te staję się ocechowane i niesprawdzone. Wieroze po tej operacji staję aię spraw -dzone. Oożoli zostanie ocechowana kolumna nie zawierejęce < Jodynki, to przechodzimy do (^) . W przeciwnym przypadku realizujemy @ .

Pytamy, czy zbiór ocechowanych i niesprawdzonych kolumn Jest pusty? Oeżeli tok, to przochodzimy do (*?). W przeciwnym przypadku, dla każdej ocechowanej i niesprawdzonej kolumny, poszukujemy znajdujęcej się w niej Jedynki i Jeżeli wierez, w którym ta jedynka aię znajduje, Jaat nieocecho -wany, to cechujemy go numerem sprawdzanej kolumny. Wiereza te staję aię ocechowane i niesprawdzone, a kolumny staję aię sprawdzone.

Przechodzimy do punktu

Pytamy, czy jest ocechowana kolumna nie zawiarajęca Jedynki? Oeżeli tak, to zwiększamy zbiór niezależnych oczek w sposób neotępujęcyi w ocechowanej kolumnie bez Jedynki umieszczamy Jedynkę w miejscu wskazanym przez cechę taj kolumny. Z wiersza, w którym umieściliśmy Jedynkę, usuwamy pozostałę Jedynkę z miejsca wskazanego przez cechę tego wiersze. W tak nowo utworzonej kolumnie bez Jedynki wstawiamy ponownie Jedynkę w miejsce wskazane przez cechę tej kolumny ltd., aż wstawimy Jedynkę do wiersza ocechowanego w pierwszym kroku

229