054(1)

258.    X²—y² = 6; j^+4y² = 16

259.    y = sinx; y = sin 2*

260.    Wiedząc, że styczna do paraboli w jej wierzchołku jest równoległa do osi Ox, znaleźć wierzchołki parabol:

1) y = x²-{-2x— 1    2) y = l+Sx-2ć 3)2y = 2x-x²

i sporządzić ich wykresy.

261.    Znaleźć punkty okręgu x¹Ą-f = 25, w których styczne są równolegle do prostej 3x+4y—12 — 0. Narysować okręg, daną prostą i styczne.

262.    Dla każdej z krzywych:

1) y = 2x?—9x²-\-\2x—5    2) y = x+ y'x

3) x = r²+l, y — 3 — t²    4) x²-f-3y^z—2x-\-6y—S = 0

znaleźć punkty, w których styczne do krzywych są rów-noległe do osi Ox.

263.    Wyznaczyć kąt, jaki tworzą między sobą dwie styczne do elipsy x = 2cos t, y = 3sinf w punktach, w których t = n\6 i t = n\3. Wykreślić elipsę i styczne.

264*. Sporządzić wykres funkcji y=|x³+x| w przedziale [-2,2] i obliczyć kąt między stycznymi w punkcie kątowym wykresu.

265. Narysować i obliczyć kąty, utworzone przez parabolę y = 2x—x² i jej cięciwę, łączącą punkty o odciętych 1 i 4.

266*. Obliczyć, jaki kąt tworzą styczne do paraboli y = x²—3x-f 1, poprowadzone z punktu (4,1). Wykreślić parabolę i obie styczne.

§ 12. Prędkość zmian wielkości zmiennej. Prędkość i przyśpieszenie w ruchu

prostoliniowym

Jeżeli wielkość z zmienia się wraz z czasem t, to prędkość, z jaką ta wielkość się zmienia, określona jest przez pochodną

Gdy znany jest związek wiążący dwie zmienne .x i y, to można określić związek między prędkościami tych wielkości, korzystając z wzoru na różniczkowanie funkcji złożonej

dy _ dy dx dt dx dt

W ruchu prostoliniowym prędkość v i przyśpieszenie w punktu określone są odpowiednio jako pierwsza i druga pochodna drogi s względem czasu t

ds    dv (Ps

267. Punkt porusza się po paraboli kubicznej 12y = x³. Która ze współrzędnych tego punktu zmienia się szybciej?

Rozwiązanie. Traktując y w równaniu paraboli jako funkcję złożoną czasu t i różniczkując względem t, otrzymamy

Stąd wyznaczamy stosunek prędkości zmian rzędnej i odciętej

dy dx _ X² dt ' dt 4

Dla x \ <2 wyrażenie to będzie mniejsze od jedności, dla ] * == 2 — równe jedności, a dla \x \ > 2 — większe od jedności. Wobec tego:

1)    gdy -2 < x < 2, rzędna zmienia się wolniej niż odcięta,

2)    gdy x = ±2, prędkość zmienności odciętej i rzędnej jest taka sama,

3)    gdy x < —2 oraz x > 2, rzędna zmienia się szybciej niż odcięta.

268. Półkulisty zbiornik, o promieniu wewnętrznym R metrów, napełniany jest wodą z prędkością Q litrów na sekundę. Obliczyć prędkość podnoszenia się poziomu wody w zbiorniku w chwili, gdy poziom wody osiągnie 0,5 R.

Rozwiązanie. Oznaczamy przez li poziom wody, liczony w metrach, a przez v jej objętość (w m³). Związek między h i v znajdziemy korzystając ze wzoru na objętość czaszy kulistej

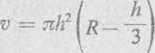
Różniczkując tę równość względem czasu t, otrzymamy związek między prędkościami zmian h i v

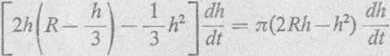
dv dv dh

dt dh dt

Podstawiając w myśl warunku

~ = 0,001 Q

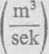
otrzymamy

dh

di

111