083(1)

6)* y = }/    — 6x²

a)    Asymptot pionowych dana krzywa nie ma.

b)    Mamy

k - lim -i _ limbZEE _{= lira}

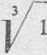
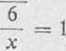
X

b = lim (y—kx) = lim ({'V—6x² —x).

_# 1

Podstawiając — zamiast x, a następnie stosując regułę de 1’Hospitala,

otrzymamy

nr	6
a^3	a^2	«/
2 -6a)'^T(-		6)
1

= -2

= lim

Tc same wartości dla parametrów asymptoty otrzymamy, gdy x -► —cc. Zatem dla a: -> -| cc oraz x -* —cc dana krzywa ma asymptolę y — x — 2.

2

Krzywa jest ciągła i przecina swą asymptotę w punkcie o odciętej ,v = y,

przybliżając się do niej od góry, gdy x- co, a od dołu, gdy * -> + oo (rys. 73).

Znaleźć asymptoty następujących krzywych :

387. y =

COS.K

388. y =

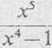
2jt—9

x+2

389. y — xe~^x

391* y = 2x-

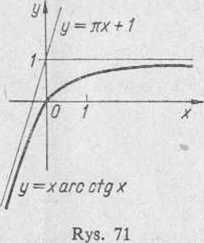
390. y = x arc tg x

392* y = ,v+ -y^V-

§ 9. Schemat ogólny badania funkcyj i sporządzania ich wykresów

Ogólne badanie własności funkcyj i sporządzanie ich wykresów wygodnie jest przeprowadzać wg następującego schematu:

I.    Wyznaczamy obszar określoności; czyli dziedzinę funkcji.

II.    Wyznaczamy punkty nieciągłości funkcji oraz granice jednostronne w tych punktach.

T1T. Badamy, czy funkcja nie jest parzysta lub nieparzysta, lub też okresowa.

IV.    Znajdujemy punkty przecięcia się wykresu funkcji z osiami układu współrzędnych oraz przedziały, w których funkcja ma stały z.nak^l).

V.    Znajdujemy asymptoty wykresu funkcji: a) pionowe, b) pozostałe.

VI.    Znajdujemy punkty ekstremalne funkcji oraz przedziały monoto-niczności.

VII.    Znajdujemy punkty przegięcia funkcji i przedziały, w których funkcja jest wypukła albo wklęsła.

VIII.    Sporządzamy wykres funkcji, wykorzystując wyniki przeprowadzonych badań. Jeśli okaże się, że informacji tych jest za mało, należy znaleźć jeszcze kilka punktów wykresu funkcji wychodząc z wyrażenia, za pomocą którego funkcja jest zadana. Dobrze jest sporządzać wykres funkcji w tej samej kolejności w jakiej następują poszczególne punkty badania funkcji.

O Wymaga to rozwiązania równania /(.v) — 0. Przy rozwiązywaniu zadań tego paragrafu punkt ten można pominąć, jeżeli rozwiązania nic można otrzymać w sposób elementarny. Ogólna metoda rozwiązywania równań będzie podana w § 10.

169