094(1)

Miejsce geometryczne środków krzywizny C{X, Y) linii nazywa się ewolutą tej linii. Równania parametryczne ewoluty dane są wzorami (2).

W stosunku do swej ewoluty krzywa wyjściowa nazywa się ewolwentą.

418.    Znaleźć krzywiznę krzywych: 1) x = t²,y — 21³ w punkcie, w któ-

.    .    71

rym t = 1, 2) y = cos2x w punkcie o odciętej x = y.

Rozwiązanie: 1) Znajdujemy pochodne: x = 2t, x = 2, y = 61²,. y = 121, obliczamy ich wartości dla r = 1

x — 2, x = 2, y = 6, y — 12 i podstawiamy do wzoru (1)

2 • 12-6 • 2

20/10

_r

(2²+6²)²

2) Z danego równania znajdujemy pierwszą i drugą pochodną >' względem x; mamy y = —2sin2x, y" = — 4cos2x. Obliczamy teraz ich wartości w danym punkcie: y |yj = 0, y" (y) = 4 i podstawiając do wzoru (1), otrzymamy

[! + (/)*]'

419.    Wyznaczyć promienie krzywizny elipsy x = acost, y — bńnt w jej wierzchołkach.

Rozwiązanie. Znajdujemy pochodne: .i: = —asinf, x = —acost, y = bcost, y = —bsinr i obliczamy promień krzywizny elipsy w dowolnym jej punkcie

3_    2_

1    (x?+.y²)^s _ (a² sin²&²cos² f)²

^W “ K{t) ^_|xy-yx\    ab

Dla wierzchołków elipsy, leżących na jej osi równej 2a, parametr t jest równy 0 lub n. Dlatego promień krzywizny elipsy w tych wierzchołkach

b¹ .

wynosi R (0) = R(n) —

Dla dwóch pozostałych wierzchołków elipsy, leżących na osi równej

3

2b, parametr t=n/2 lub t = —n. W wierzchołkach tych promień krzy-/ n \    13n \ a¹

wizny elipsy wynosi R I ₂ 1 = R (-yl = -g.

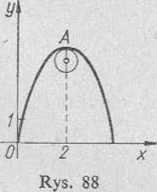
420. Znaleźć współrzędne środka krzywizny i wykreślić krzywe oraz kola krzywizny krzywych: 1) y — 4x—x² w jej wierzchołku, 2) x = t—sin?, y = 1—cos? w punkcie, w którym ? = ?r/2.

Rozwiązanie: i) Równanie to przedstawia parabolę o osi równoległej do osi Oy. Wierzchołek jej znajdujemy z warunku, że styczna jest tam równoległa do osi Ox\ czyli z warunku y' — 0. Mamy

y' = 4—2.xr, y' = 0 dla x = 2,    y(2) = 4

Następnie ze wzorów (2) znajdujemy współrzędne środka krzywizny C danej paraboli w jej wierzchołku (2,4)

X= x-

1+00²

/=2,

r = y-

l+OT

7

2

oraz kreślimy parabolę i koło krzywizny w^r jej wierzchołku (rys, 88).

2) Znajdujemy pochodne i=l— cos?, 3ć = sin?, y = sin?, y = cos? i obliczamy ich wartości, gdy ? = nj2. Mamy

if)-'-    >(tH

Ze wzorów (2) obliczamy współrzędne środka krzywizny

X = x-

^x>y o_ ⁷¹ ,,

-1

xy-yx

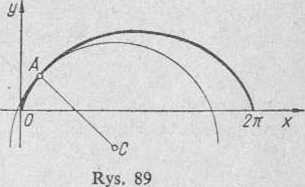
Następnie wykreślamy daną cykloidę; zaznaczamy punkt — — 1; lj> odpowiadający wartości ? = .t/2, i znaleziony środek krzywizny c{-^ +1; — lj oraz kreślimy koło krzywizny (rys. 89).

591