10cz4

*3.26. Uzasadnij, że odcinek łączący środki przekątnych dowolnego trapezu jest równoległy do podstaw i jego długość jest równa połowie różnicy długości podstawi ;

V

10-

\<c

I I

iii

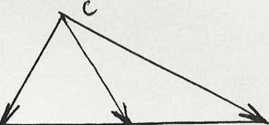
*3.27. W trójkącie ABC bok AB ma długość c. Punkty M, N leżą odpowiednio ^:na bo- i kach CA \ CS tak, że \CM\ : \MA\ = \CN\ : \NB\ =2:1. Wyznacz długość odcina i

^MN•    _c

(Przykład 16. Wektory a i ó są równolegle. Oblicz współrzędne wektora b, gdy CA.    i a = [2,-l] i |£| = 2V5.    b

Rozwiązanie. Ponieważ wektory a i ó są równoległe, więc istnieje liczba rzeczywista k, taka że k-a-b . Zatem = fc-[2,--l], czyli ó=[2A:,-/:].

. . . . , jNiieo^ AlbC bedbjue    _l pu/wioP U -

tweicbovow C cłb _>

*?U9 _t

iolouOOWn. i wt eAob.^rwe, :    _

^A .    . _v rv /o ^ p)

10 dloa^oW^rrrv    e»vo^tov^e peu^u?_c £

tv    TOU/rOccue* | U<óv\^ cmAeAO    a ^cA\P o-s

VI2/    Wl—. -C

^XoxęAvUx ^: Ab, fbE, CP - Wu>Kt

a r>foc

t|ć*łqA fłDnbEnCF-{°l

lo&l _ IOE) IOFI ₌ ■*

)0ft| " (Oftp 10C| ~ X

* *> /bo

(Ujdo^wodA^j t wn eAOb^rw^ :

IfeA^U, w cU>vvoIawi/yvv ŁwDiłoot^    Ow^cUou

oUopoIaw^ dt^ócK^J bokjó& ₍4o    odoi'vwe(o

<^^_jtv^ec0eX2O bc>\^^ C jex>o olCL^o^sc ^sia^4-    potowa    icdkoJL tneCcif/O .

6

ĆwiczeniCS)Sprawdź, czy wektory /łfi i CD r.ą równoległe, gdy: /I ( 3,2),_: .. 5 = (5,4), C = (1,2), D = (5,3).

ĆwiczeniCiJ) Wykaż, że czworokąt ABCD o wierzchołkach: A = (1,2), 5 - (-1,4),

C = (0,0), D = (2, - 2) jest równoległobokiem.

|£| = 2 V5 i |^| = V(2A')² + (-^')² > czyli ^4k²+k² = 241,

-JŚJ? = 2J5 <=> |/c| = 2 <=> /c = -2 v k = 2 .

Zatem D = —2 [2, -1] lub D = 2 - [2, —l].

Odp.: 6 =[-4,2] lub b=[4,-2].

FĆwiczeniśCSDwektory u i S są równoległe. Oblicz współrzędne wektora gdy

' Ofltp.U^Cf-20|

M =

-2V2,

i |S| = 5,

aiii

i3.24?)Wiedząc, że z! = (-2,3), B = (1, - 2), C = (4,5), oblicz współrzędne i d^gof&|

I wektora w, gdy:

la) w=AB+BC,    b) w = {m + ~Ac)+{aB-bĆ)]

c) w = Jb + BC + CA, [Ojd] _f O    |(i) b=AC-(^tfBc), '[o,^ / %$!!;•’;•

e) w=2Tb~3AC, fU^G] _}2D    F 0 w = -2(^ + Aę)+3(AB-BC). 'W'**?':

13.25.yWiedząc, że A = (3,-2), fi = (1,3), C = (-2,5) i D = (-4,-2), oblicz współrzędne punktu E spełniającego warunek EA + EB + EC + ED = 6.    <*fe(-£y|)

^13.26j)Punkty M i N dzielą odcinek AB na trzy równe F części. Oblicz współrzędne punktów M i N, gdy    /

^ = (2,1),i s=(u,4). Oip- M(S)i)_} N(8,b)

(oirTi)

•A

M N

Wektory a i b są równoległe. Oblicz współrzędne wektora b , gdy:    \

_r , _r.    (T-ft;śi\ _    .    ' (t»-cwrwq

a)_a=[-i,3] 11*|=vm,!-i]/ P ^b> «=[2,-4] 11*|=vtó, (f*.•,

c) 5 = [I,5] i U = 2,

TM. fe.5xlR'iaT    ^

•>. A r. O ri----- -s ^ »- f\ - f- A A DL - I <V . >

robot PHbc-O o kjol

A On m.

c>v

\ri -rC^M