matma1 2

1. Pole trapezu jest równe 40 cm², a odcinek łączący środki ramion trapezu ma długość 5 cm. Wysokość tego trapezu ma długość:

a)4 cm    b)8 cm    c)12 cm    d)16 cm

2. Pole pewnego czworokąta wypukłego wynosi Miara kąta przecięcia przekątnych jest równa: a)30°    b)45°

35, a jego przekątne mają długość 10 i 14.

c)60°

d)90^c

3. Obwód koła K jest o 40% większy od obwodu koła K_v Pole koła K jest większe od pola koła Kx o:

a)16%    b)20%    c)40%

d)96%

4. Wysokości równoległoboku mają długość 12 cm i 8 cm, a dłuższy bok ma długość 15 cm Krótszy bok ma długość:

a)6cm    b)9cm    c)10 cm    d)ll cm

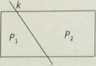
c)3 : 7

d)5:

5. Na rysunku obok prosta k dzieli jeden dłuższy bok prostokąta na odcinki, których długości pozostają w stosunku 1 : 5, a drugi dłuższy bok dzieli na połowy. Stosunek pól Pi : P₂ powstałych w ten sposób trapezów wynosi:

a)l: 2    b)2 : 5 9

6. (2p.) Na rysunku obok znajduje się plan działki, wykonany w skali 1 : 4000. Wiedząc, że na planie droga AB ma długość 2,5 cm, a powierzchnia czworokąta wynosi

7— cm², oblicz:

4

a)    rzeczywistą długość drogi (w m)

b)    rzeczywistą powierzchnię działki (w m²).

7.    (3p.) Różnica pól dwóch kwadratów jest równa 19. Oblicz długości boków tych kwadratów, wiedząc, że wyrażają się one liczbami naturalnymi.

8.    (4p.) W trapezie kąty ostre przy dłuższej podstawie mają miary 45° i 30°. Krótsza podstawa ma długość 6 cm, a długość dłuższego ramienia wynosi 8 cm. Oblicz pole tego trapezu. Wynik podaj w przybliżeniu dziesiętnym z dokładnością do 0,1 cm².

9.    (6p.) W rombie ABCD o polu 216 cm² poprowadzono odcinek EF długości 9 cm, którego końcami są odpowiednio środki boków BC i DC, tworzących kąt ostry rombu. Oblicz:

a)    długości przekątnych rombu

b)    długość wysokości rombu

c)    pole pięciokąta ABEFD.