10 (27)

178

9. Funkcje wielu zmiennych

Jeżeli/jest funkcją rzeczywistą o dziedzinie (a, b) <= R^l oraz x e (a, b), to pochodna f'(x) jest zazwyczaj określana jako liczba rzeczywista

h~0 h

oczywiście pod warunkiem, że ta granica istnieje. Zatem

(8)

f(x+h)-f(x) = f'(x)h+r(h),

gdzie „reszta” r(/i) jest mała w tym sensie, że

(9)

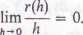
Zauważmy, że we wzorze (8) różnica f(x+h)—f(x) wyrażona jest jako suma funkcji liniowej przekształcającej h w f\x)h i małej reszty.

Możemy więc tu traktować pochodną / w punkcie x niejako liczbę rzeczywistą, lecz jako operację liniową na R^l przeprowadzającą h w f'(x)h.

(Zauważmy w związku z powyższym, że każda liczba rzeczywista określa operator liniowy na R^l — mianowicie operator, który polega po prostu na pomnożeniu argumentu przez tę liczbę. Odwrotnie — każda funkcja liniowa na R¹ i o wartościach w R¹ jest operacją mnożenia przez ustaloną liczbę rzeczywistą. Istnieje więc naturalna 1:1 odpowiedniość pomiędzy R¹ i HR¹), która uzasadnia opisane spojrzenie na pochodną.)

Rozważmy teraz funkcję f odwzorowującą {a, b) c R¹ w R^m. W tym przypadku określiliśmy f'(x) jako wektor y e R^m, (o ile taki istnieje), dla którego

(10)

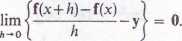
Także i teraz możemy przepisać ten warunek w postaci

(11)

f(x+A)-f(x) = hy+r(h),

gdzie r(h)/h-*0 przy h-*0. Pierwszy składnik po prawej stronie (11) jest znowu funkcją liniową argumentu h. Każdy y e R^m wyznacza liniowe odwzorowania R^l w R^m, poprzez przyporządkowanie elementowi he R¹ wektora hy e R^m. To utożsamienie R^m z L(R‘, R^m) umożliwia nam traktowanie f'(x) jako elementu L(R^l, R^m).

Zatem, jeżeli f jest odwzorowaniem różniczkowalnym (a, b) ć R¹ w i?"¹ oraz x e (a, b), to /'(x) jest przekształceniem liniowym R¹ w R^m spełniającym

(12)

_limUx+h)-f(x)-f’(x)h

*-o    h

= 0

lub równoważnie

(13)

|f(x+/j)-f(x)-f'(x)/i| lim-—,-

| 0.