11164658�4734582268562�50946466917580996 o

^ 420MPa

Problem 2. Załóżmy, że funkcja ugięcia płyty prostokątnej o wymiarach 2 x 2 wyraża wzorem: w(x,y) = 2(x² + xy + y²). Obliczyć funkcję spaczenia = -2—^

(Uwaga: pytanie za podwójne punkty)

Problem 3. Podać definicję momentu skręcającego m_xy.

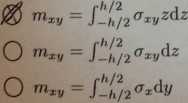
Problem 4. Jakie tensory w teorii plastyczności wiąże ze sobą tensor Hooke’a w sposób wzi jemnie jednoznaczny?

j^) Prędkość naprężenia & i prędkość odkształcenia sprężystego e^e.

O Prędkość naprężenia & i prędkość odkształcenia platycznego e^p.

O Prędkość naprężenia & i prędkość całkowitego odkształcenia e.

Problem 5. Czym różni się od liniowej teorii płyt cienkich teoria von Karmana?

O Uwzględnieniem umiarkowanie dużych ugięć przez uzależnienie momentów zgina

jącycli od krzywizn i spaczenia.

ig) Uwzględnieniem umiarkowanie dużych ugięć przez uzależnienie odkształceń po wierzchni środkowej od gradientów ugięcia.

O Uwzględnieniem umiarkowanie dużych momentów przez uzależnienie ich od od-kształceń membranowych.

(). I)la 1 iniowej teoiii sprężystości obliczono MES wektor węzłowych przemieszczeń w elemencie u^e. Przyjmując oznaczenia N - macierz funkcji kształtu, L - macierz W dowolrvmTuIdn£eirtuV ““ Hooke^a, z jakiego wzoru oblicza się tensor naprężenia