121(1)

(obszar C'3D leży poniżej osi Ox, aby więc jego wartość miała znak dodatni, granice całkowania zostały wzięte od strony prawej ku lewej) .

Sa^o = I (**-2x)dx = £-y- _t = — + 1 = y Wobec tego S = 9+ y — ~ — 9.

Pole S można też obliczyć inaczej, określając różniczkę dS jako pole prostokąta o wysokości równej różnicy rzędnych obu parabol i o podstawie dx (rys. 97). Wtedy

dS = (y_l—y₂)dx = [(4 - X²) — (x⁷-—2x)] dx = (4+2x—2 x?)dx

skąd

S = J (4+2*-2x²)dx =    -ł jc³ J =9

J) Znajdujemy trzy punkty przecięcia się danych parabol: 0(0,'0), A(0, —4), 5(0, 4), a następnie sporządzamy wykres (rys. 98).

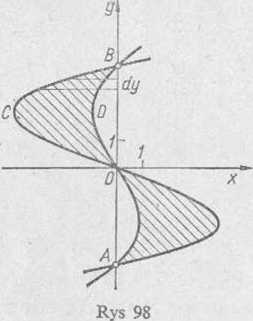
Szukane pole składa się z dwóch równych części. Połowę pola S można obliczyć jako różnicę pól dwóch trapezów krzywoliniowych OCB i ODB, przylegających do osi Oy. Na podstawie wzoru (2) mamy

o    o

Socb = j'*\dy = y J (y^?—l6y)dy

4    4

2    i ⁰

Sodb = J *2dy — — j (y³-16y)dy

4    4

oraz

° 1 °

S = 2(Socb—Sodb) = 2 j    — x₂)dy = — j (y¹—16y)dy —

4    4

= T [4 “⁸^J ⁼ T (“⁶⁴+¹²⁸) = ¹⁶

4) Osie układu współrzędnych pokrywają się z osiami symetrii danej elipsy (rys. 99) i dzielą ją-na cztery równe części. Czwartą część szukanego

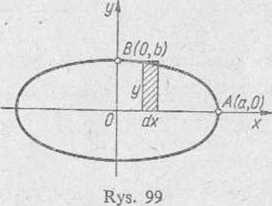
pola S, leżącą w pierwszej ćwiartce płaszczyzny, znajdujemy obliczając pole odpowiedniego trapezu krzywoliniowego, przylegającego do osi Ox

⁼ J y^dx

O

Ponieważ elipsa dana jest równaniami parametrycznymi, więc całkę przekształcamy tak, aby zmienną całkowania był parametr t. Podstawiamy y ~ ósinr, dx = — a sin tdt i ustalamy odpowiednie granice całkowania:

dla x — 0, ł = ~i dla x = a, t — 0; wtedy

a    o

S = 4 I ydx = —4ab f sia²tdt =

— 2ab J (1 — cos 2t)dt = lab    sin2?J² — ziąb

245