137(1)

Stosując podstawienie } II—x = r, otrzymamy dx = —2zdz oraz r, — )/ H dia x = 0 i z₂ = J H—h dla x = /;, cz>'li

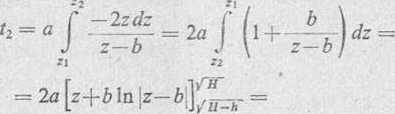
Przebieg zmiany poziomu wody w zbiorniku może być tu dwojaki. Jeżeli w chwili początkowej, gdy h = 0, natężenie przypływu wody V będzie mniejsze od natężenia wypływu wody ze zbiornika, równego 0,6rj. 2gH, to poziom wody będzie obniżał się dotąd, dopóki obie te wielkości nie staną się równe. Z chwilą ich wyrównania się poziom wody nie będzie się zmieniał. Poziom ten będzie mniejszy od początkowego poziomu H o wielkość h_l określoną równaniem: Q.6s\/2g(H—Aj) — V.

Jeśli natomiast w chwili początkowej V > 0,6s| 2gII, to poziom wody w zbiorniku będzie się podnosił dotąd, dopóki nie przewyższy początkowego poziomu H o wdelkość /j₂ określoną równaniem: 0,6s\. 2g(R+h₁) = = V, po czym poziom wody w zbiorniku będzie stały.

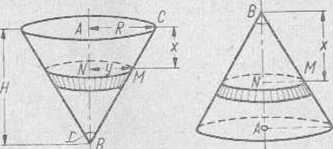
667. Dwa równe naczynia mają kształt prostych stożków kołowych o osi pionowej. Wymiary stożków i ich położenia są podane na rys. 131. Oba naczynia napełniono wodą, która następnie wypływa przez niewielkie jednakowa otwory kołowa w dnie naczyń.

C

Rys. 131

W ciągu jakiego czasu woda wypłynie całkowicie z każdego naczynia i w jakiej chwili poziomy wody w obu naczyniach będą jednakowe, jeżeli z obu naczyń woda zaczyna wypływać jednocześnie?

Rozwiązanie. Przyjmujemy, że czas t, w ciągu którego poziom wody w pierwszym lub w drugim naczyniu opadnie o x, jest pewną funkcją /(x) i znajdujemy jej różniczkę dt, gdy x zmienia się o dx.

Niech opadnięciu poziomu wody w naczyniu o małą wielkość dx odpowiada mały przyrost czasu A t. Zakładając, że w tym małym odstępie czasu woda wypływa z naczynia ze stałą prędkością, równą 0,6 \ 2g(H—x), znajdujemy, że objętość wody, wypływającej w czasie At przez otwór w dnie naczynia o przekroju nr², wynosi

A V » 0,6nr² y^/2g(H-x) A t

W tym samym odstępie czasu At objętość wody w naczyniu zmniejszy się o AV\ ~ vr.y²dx, przy' czym wielkość ta powinna być równa objętości wody wypływającej z naczynia. Z równości AV — AV, otrzymujemy

Al.

— dt

y²dx

0,6r² j/2g(H—x)

Czas, potrzebny na opróżnienie pierwszego i odpowiednio drugiego zbiornika, otrzymamy przez scałkowanie dt w granicach od x = 0 do x = H

fdx

0,6r² y'2g J j II-

Aby obliczyć tę całkę wyrażamy zmienną y przez zmienną x. Ponieważ trójkąty ABC i NBM (rys. 131) są podobne¹), więc:

a)    dla pierwszego naczynia _R- = ——; y = -jj(H—x)

Jhf x    R

b)    dla drugiego naczynia = —; y == — x

Wobec tego czas t_t potrzebny na całkowite opróżnienie pierwszego naczynia wyniesie

U =

R^2	F (H~x)
0,6r^2H^21 2g .	^1 1 H-*
R^2	2(H-x)
0,6r^2H^21 2g	5

d.x —

3r² \

H

2 V

') Ponieważ z założenia r jest bardzo małe w. porównaniu z pozostałymi wymiarami naczynia, to dla uproszczenia obliczeń przyjmujemy, że przekrój osiowy naczynia ma ksztait trójkąta, a nie trapezu.

277