172(1)

823. Obliczyć objętości brył ograniczonych powierzchniami: y— 1, x+y+z = 4,    2 = 0

2)    r = y²-x\ z = 0, y = ±2

3)    z = 4-;t²-y\ 2z = 2+x²+y²

4)    J^-f^+r² = R¹, z = a, z = b; R> b> a> 0 Rozwiązanie: 1) Daną bryłą (rys. 171) jest pionowy walec, ograniczony od góry płaszczyzną z = 4—x—y, a od dołu — częścią płaszczyzny xOy, zawartą między parabolą y — x² i prostą y ~ 1.

z

Rys. 171

Zgodnie ze wzorem (a) objętość tej bryły wynosi

i y7

V= IJ zdxdy = j dy j (4—x—y)dx =

O AB    o -j/JT

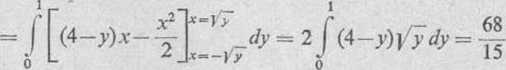
i    i

Przy' całkowaniu w odwrotnym porządku, mamy

68

"15

V= j dx j (4—x—y)dy = ... = ~

2) Paraboloida hiperboliczna z = y²—x² przecina płaszczyznę xOy (z = 0) wzdłuż dwóch prostych y — Wraz z płaszczyznami z = 0 i y = ±2 paraboloida ta ogranicza bryłę symetryczną względem płaszczyzn

\0z i yOz. W myśl wzoru (a) objętość czwartej części bryły, leżącej w pierwszej ósemce (w pierwszym oktancie) przestrzeni (rys. 172), dana jest całką

dy =

oab    oo    o ^u

3) Bryłę ograniczoną danymi paraboloidami obrotowymi przedstawiono na rys. 173. Objętość jej znajdujemy jako różnicę' objętości dwóch brył

Rys. 172

Rys. 173

cylindrycznych ograniczonych z góry danymi powierzchniami i mających za podstawę jeden i ten sam obszar D, leżący .na płaszczyźnie xOy

V=V₁-V2 =

( f(4-x²-f)dxdy- j ( y(2+x*+y²)dxdy

D

D

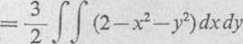
D

Linia L przecięcia się danych powierzchni dana jest układem równań obu tych powierzchni: z = 4—x²—y², 2z = 2-rX²-f-.y².

Eliminując z tego układu z, otrzymamy a^+J² = 2. Jest to równanie pionowej powierzchni cylindrycznej przesuniętej przez linię L i rzutującej ją na płaszczyznę xOy. Otrzymane równanie jest jednocześnie równaniem

347