1 (52)

58

3. Ciągi i szeregi liczbowe

1

⁺^+iT^f*-

tak że

(16)    0 < e—s„ <

n!n ,_H

W ten sposób suma s₁₀ przybliża liczbę e z błędem mniejszym niż 10“ ⁷. Nierówność (Ij^ ma wartość teoretyczną, bo pozwala łatwo udowodnić, że e jest niewymierne.

3.32,    Twierdzenie. liczba e jest niewymierna.

Dowód. Przypuśćmy, że e jest liczbą wymierną. Wówczas e = pfą, gdzie p,q są liczbami naturalnymi. Z (16) mamy 0 < ql(e—s_ę) < K Zgodnie z założeniem, q\e jest liczbą całkowij tą. Liczba g!(e—s₄)jest także całkowita, ponieważ

Ponieważ q > 1, z (17) wynika istnienie liczby całkowitej leżącej między 0 a 1. W ten sposón doszliśmy do sprzeczności.

Inne kryteria zbieżności

3.33.    TWIERDZENIE (kryterium Cauchy’EGO). Niech dany będzie szereg i niech] a = lim sup (/jaj". Wówczas:

Ił ^ Op .

a)    jeśli a < 1, to j^a„jest zbieżny;

b)    jeśli a » 1, to £a„jest rozbieżny;

c)    jeśli a = 1, to szereg jest zbieżny lub rozbieżny.

1

1

pMP ( h+2)! («+3) !

• mm

i+

n+ł

I M jestrozbieżn, I Dowód. Jeśli zi < P dla n >

pnączy to, że

■a n > N i a) wyni I Jeśli |a_n+1| > |o. Ignika b).

I Uwaga. Ze zna kręgu £a„. Przyfc

I 3.35. PRZYKŁAI lego

Dowód. Jeśli a < 1, to możemy wybrać fi tak, aby « < /? < 1 i liczbę całkowitą N taką, aby (/jaj < /? dla n > N (z twierdzenia 3.17b)). Inaczej mówiąc, dla n & N mamy jaj < /?". Szereg ^ jS" jest zbieżny, ponieważ 0 < fi < 1. Zbieżność szeregu £a„ wynika teraz z kryterium porównawczego.

Jeśli a > 1, to znowu z twierdzenia 3.17 istnieje ciąg {«*} taki, że (/ląj -> a. A więc ja„j > 1 dla nieskończenie wielu wartości n, stąd warunek a„ -» 0 konieczny dla zbieżności szeregu pfc nie jest spełniony (twierdzenie 3.23).

ale pierwszy jest rozbieżny, a drugi zbieżny.

Aby udowodnić c), rozpatrzmy szeregi

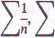
-j. Dla każdego z tych szeregów a = 1, n

3,34. Twierdzenie (kryterium dAlemberta). Szereg ^a„ a) jest zbieżny, jeśli lim sUp -iii <1;

lim inf

n-*co

lim sup—

*-»oo a

Kryterium Cauchy aozstrzygnięcia.

b) To samo jest [+..., gdzie

limirt

336.    UWAGL Ki ponieważ łatwiej jest jest jednak silniejsze i kryterium Cauchj i kryterium d’Alemb przykładami.

Żadne z tych kr rozbieżność wynika

337.    Twierdze