1 (58) 3

64

3. Ciągi i szeregi liczbowe

Y,    i Y b„2? wymnożymyje podobnie jak wielomiany i zgrupujemy wyrażenia pod

otrzymamy

( Y ^an^)( Y bnZ") = (a₀+ai2+a₂z²+...)(6o+6₁z+6₂z²+...) =

^s Mo+Wl +    +    + ^2^ofe²+... s ]

= c₀+c₁z+ę₂z²+...

Przyjmując z — 1, otrzymujemy podaną wyżej definicję. 3.49. Przykład. Jeśli

A„ « i a*, B_n= i bi, C'=tck

k-0    k=0    Jt = 0

i ,4„-*.4,    to nie jest całkiem jasne, czy ciąg {C„} jest zbieżny do ,45, ponieważ nil

prawdą, że C_n = Zależność {C„} od {/!„} i {B„} jest bardzo złożona (patrz doi twierdzenia 3.50). Udowodnimy teraz, że iloczyn dwóch szeregów zbieżnych może rozbieżny. Szereg

Zjy/n+T

jest zbieżny (twierdzenie 3.43). Konstruując iloczyn tego szeregu przez siebie, otrzymujeM

Y?^m 1 _ Oz⁺J2)⁺(j!⁺jtjiji)(ję⁺    + j£ji'⁺

tak że

Ponieważ

(n-k+M+1) m (i«+l)²-(>-k)² < &1+I)²,

mamy

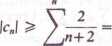
*-0

2(n+t)

n+2 a więc warunek c„-*0, konieczny dla zbieżności szeregu Y^c*> jW spełniony.

W związku z następnym twierdzeniem pochodzącym od Mertensa, zauważmy, że rozpatrywaliśmy w tym przykładzie iloczyn dwóch szeregów zbieżnych warunkowo.