1tom139

6. ELEKTROTECHNIKA TEORETYCZNA

280

Dwa zaciski należące do dwóch różnych cewek sprzężonych magnetycznie nazywamy zaciskami jednoimiennymi i oznaczamy jednakowymi wskaźnikami, jeśli przy jednakowym zwrocie prądów względem tych zacisków strumienie magnetyczne indukcji własnej i wzajemnej w każdej cewce mają jednakowe zwroty. Na rysunku 6.8 zaciski jednoimienne oznaczono gwiazdkami. W obwodach elektrycznych, w których istnieje sprzężenie magnetyczne elementów indukcyjnych, występują napięcia indukcji wzajemnej.

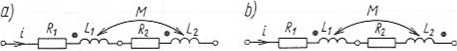
Ul    U₂    U,    _U2_

Rys. 6.8. Dwie cewki sprzężone połączone szeregowo: a) zgodnie; b) przeciwnie

Przy przebiegach sinusoidalnych — analogicznie jak dla indukcyjności własnej mamy reaktancję indukcji własnej X, = cjL — dla indukcyjności wzajemnej wprowadzamy reakiancję indukcji wzajemnej

X_M = co M    (6.42)

lub impedancję indukcji wzajemnej

Z_M= }X„    (6.43)

Odpowiednio napięcie

Um = Z_m1    (6.44)

Przykładowo, jeśli dwie cewki o indukcyjnościach własnych L, i L₂ oraz rezystancjach odpowiednio R, i R, są sprzężone magnetycznie i połączone zgodnie (zgodny jest kierunek nawinięcia), rys. 6.8a, to

U_ = R₂ J_+)coL_lI^+jcoMJ^ + R₂J[+}CoL₂I^+j(oMl = [R₁+R₂+j(coi.₁ +

+coL₂+2coMJ]I    (6.45a)

Jeśli połączenie jest przeciwne (przeciwny jest kierunek nawinięcia), rys. 6.8b, to

U = R_xl+icoL_ll_—jcoM ]_+ R_z]_+)<oL₂I_—')(x>M1_ = [R₁ + R₂+j(coL_l +

+coL₂-2coMj]l    (6.45b)

Występowanie indukcyjności    wzajemnej przy'    zgodnym połączeniu cewek    zwiększa

indukcyjność układu,    a    przy    przeciwnym połączeniu    cewek    zmniejsza    indukcyjność

układu. W pierwszym przypadku reaktancja układu wzrasta, a w drugim — maleje.

6.3. Obliczanie obwodów rozgałęzionych

6.3.1. Pojęcia podstawowe

Przedmiotem rozważań będą obwody liniowe, stacjonarne o parametrach skupionych, zawierające elementy R, L, C, M oraz źródła niesterowanc. Każdy tego typu obwód może być rozwiązany przy zastosowaniu dwóch praw KirchhofTa, jeżeli są znane parametry elementów tworzących dany obwód. W celu wyznaczenia rozpływu prądów i rozkładu napięć w obwodzie konieczna jest ponadto znajomość struktury obwodu. Przez topologię obwodu należy rozumieć te jego właściwości, które dotyczą sposobu połączenia elementów tworzących daną strukturę. Pojęciami podstwowymi w dziedzinie topologii są pojęcia gałęzi i węzła.

Gałąź obwodu elektrycznego tworzy jeden lub kilka połączonych ze sobą elementów. Cechą charakterystyczną gałęzi jest jej prąd.

Węzłem obwodu elektrycznego nazywa się końcówkę (zacisk) wyprowadzoną na zewnątrz, do której jest lub może być przyłączona następna gałąź lub kilka gałęzi. Cechą charakterystyczną węzła jest jego potencjał.

Każda gałąź obwodu jest ograniczona parą węzłów. Przyjmiemy, że liczba gałęzi obwodu wynosi b, a liczba węzłów v. Jeżeli każdej gałęzi łączącej dwa węzły przyporządkujemy odcinek niezorientowany, to otrzymamy strukturę geometryczną zwaną grafem niezorientowanym (strukturalnym). Przy tworzeniu grafu idealne źródła napięcia traktujemy jako zwarcia, a idealne źródła prądu jako przerwy.

Jeżeli w obowodzie oznaczymy zwroty prądów w gałęziach, to obwodowi takiemu można przyporządkować graf zorientowany.

Na rysunku 6.9a przedstawiono obw-ód rozgałęziony o liczbie gałęzi b = 6 i o liczbie węzłów v = 4; przedstawiono także graf niezorientowany tego obwodu (rys. 6.9b) oraz graf zorientowany (rys. 6.9c).

Rys>. 6.9. Obwód rozgałęziony: a) schemat obwodu: b) graf niezorientowany; c) graf zorientowany

Oczkiem grafu jest nazywane takie następstwo gałęzi, przy którym węzeł początkowy i węzeł końcowy są identyczne, a pozostałe węzły występują jeden raz. Na rysunku 6.9c są podane zwroty obiegowe oczek. Liczba oczek niezależnych w grafie jest równa b — v+ 1, a więc dla obwodu z rys. 6.9c liczba oczek niezależnych wynosi 6—4+1 = 3.

63.2. Metoda klasyczna (praw Kirchhoffa)

Metoda klasyczna polega na obliczaniu rozpływu prądów w obwodzie rozgałęzionym poprzez rozwiązanie układu równań, napisanych dla obw'odu zgodnie z pierwszym i drugim prawem Kirchhoffa.

Dla obwodu z rys. 6.9 zgodnie z pierwszym prawem Kirchhoffa można napisać c— 1 = 4—1 = 3 równania niezależne. Równania te dla węzłów 1, 2 i 3 mają postać

dla węzła 1 h — I2+I3

dla węzła 2    = /, + J₆    (6.46)

dla węzła 3    _/₂ +_f₅ = ł__A

Zgodnie z drugim prawem Kirchhoffa można napisać ó—(t>—1) = 6—4+1 = 3 równania niezależne. Równania te dla oczek, dla których na rys. 6.9c są podane zwroty obiegowe oczek, mają postać

(6.47)

^i-K2 = z₁i_₁+z_si₄+z₁i₂ Ężl+Rs — Z₃_f₃ —Z,_/j + Z₅_/₅