221

0 < 90°), czy też niezwilżającą (0 > 90°). W pierwszym przypadku siły adhezji (przylegania) są większe od sił kohezji (spójności), w następstwie czego wypadkowa sił oddziałujących spowoduje podniesienie się cieczy na krótkim odcinku wzdłuż ścian naczynia.

Jeżeli, z drugiej strony, oddziaływanie między cieczą a powierzchnią ciała stałego polega na odpychaniu (siły kohezji są większe od adhezji), to powierzchnia cieczy (menisk) przybierze kształt krzywizny skierowanej w dół. Jeżeli odległość pomiędzy dwiema równoległymi ścianami naczynia jest równa lub mniejsza od promienia krzywizny menisku cieczy, to obserwuje się zjawisko podciągania kapilarnego (rys. 3.53). Wielkość h można wyrazić również liczbami ujemnymi dla cieczy niezwiiżających ścian naczynia (obniżenie poziomu cieczy).

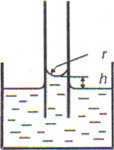
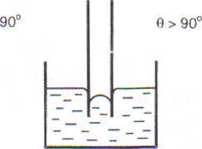
Rys. 3.53. Zachowanie się cieczy niezwilżającej i zwilżającej w kapilarze Wysokość, do której podnosi się poziom cieczy w kapilarze h, określona jest równaniem

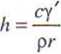
(3.102)

gdzie:

h

c

/

y

p

r

wysokość podciągania kapilarnego, m; stała;

napięcie powierzchniowe cieczy, N/m; gęstość cieczy, kg/m³; promień krzywizny, m.

W 1921 r. Washburn pierwszy zasugerował użycie rtęci pod ciśnieniem do określenia rozkładu porów dla porowatych soli. Rtęć posiada bowiem przeciętny kąt zwilżania ciał stałych w temperaturze pokojowej około 140°, co gwarantuje uniknięcie zjawiska podciągania kapilarnego. Opór ten może być przezwyciężony przez ciśnienie zewnętrzne. Zależność między rozmiarem porów r, do których może wniknąć ciecz, a zewnętrznym ciśnieniem p na nią wywieranym, wyrażona jest następującym równaniem

	27try'cos0 = rcr^2p	(3.103)
r	- promień porów, m;
P	- ciśnienie, N/m^2;
0	- kąt zwilżania, deg.

a po uproszczeniu

pr = 2y'cos0    (3.104)

221