236(1)

Rozwiązanie tego zadania znacznie się uprości, gdy skorzystamy z zespo- ^ lonej postaci (4) całki Fouriera

+ 00    +®

= J tr^mdn J q(t)e^l"dt =

«.    —CO    — °0

+ 00 1

=    | te^la,dt =

— co    O

«•“(! -/«)—1

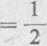
+ oo /

Oczywiście, powyższe przedstawienie funkcji za pomocą całki Fouriera w postaci zespolonej i otrzymane wcześniej jej przedstawienie za pomocą <-?łVi Fouriera w zwykłej postaci różnią się tylko formalnie i można je przekształcać jedno w drugie, korzystając z wzorów Eulera.

Przedstawić za pomocą całek Fouriera oraz sporządzić wykresy riastę-puiących funkcji:

1056

(sin

•Ho,

[co:

•² = 10,

(sinx, gdy |x| < n gdy |xj ^ n (cos*, gdy O < x < n gdy x>n

1057. u =

1058. v =

1+*, gdy — 1 <* <0 1—*, gdy O < x< 1 O, gdy |x| > 1 O, gdy x < O sin x, gdy O < x < n O, gdy x ^ n

RÓWNANIA RÓŻNICZKOWE

Głównym celem inżyniera lub naukowca, badającego dowolny fizyczny lub techniczny proces, jest wykrycie prawidłowości rządzących tym procesem i znalezienie analitycznych wyrażeń dla zależności funkcyjnych, wiążących zmienne parametry tego procesu.

Większość zadań, polegających na odnalezieniu związków pomiędzy zmiennymi, sprowadza się do rozwiązywania równań zawierających albo pochodne, albo różniczki niewiadomych funkcji.

Ogromne znaczenie tych zadań, zarów no w praktyce jak i w badaniach teoretycznych, decyduje o tym, że ten dział analizy matematycznej jest szczególnie ważny.

§ 1. Równania różniczkowe. Rząd równania.

Całka ogólna i całka szczególna

Równaniem różniczkowym nazywamy równość zawierającą pochodne albo różniczki niewiadomej funkcji.

Jeżeli niewiadoma funkcja zależy tylko od jednego argumentu, to rów-, nanie różniczkowe nazyw'a się zwyczajnym. Gdy natomiast funkcja ta zależy od kilku argumentów (jest funkcją wielu zmiennych), a równanie różniczkowe zawiera jej pochodne cząstkowe względem tych argumentów, to nazywamy je równaniem o pochodnych cząstkowych albo krócej równaniem różniczkowym cząstkowym. Równaniom takim poświęcamy ostatni paragraf tego rozdziału, wcześniejsze paragrafy poświęcone są natomiast równaniom zwyczajnym.

Rzędem równania różniczkowego nazywamy rząd najwyższej pochodnej występującej w tym równaniu. Na przykład:

475