247

492 Rozwiązania i odpowiedzi

18.128.    / = ln |e* + 5|.    18.129.

I = x-ln |2e* + l|+Ve²*T4e^r+j x>0, x^l ; / = ln |ln x|.

/ = Jc((In |x|)² —2 ln |x|+2). / = i(2 + 5x)(ln |2 + 5jc| —1).

/= _1 (ln |x|+l).

18.130.    / = ln    18.131.

18.132.    / = i ,/5 arcsin (s/| e^x).    18.133.

18.134.    I=-e~^x(x³ + 3x²+6x+6).    18.135.

18.136.    / = xln |x² + l| — 2x + 2 arctgx .    18.137.

18.138.    / = jeln |^ + Vjc²+1|-7jc² + 1 .    18.139.

18.140.    /=arctg(ln |jc|).    18.141.

DO ROZDZIAŁU XIX

19.5.	/ =	CłH*^2 — 4|]»-iln^.	19.6.	ri xT n [= — arctg— ' = —. L ^a a Jo ^4«
19.7.	/ =	[-^]>	19.8.	^1 = tło ^arctg l^xY-'ls =
		r 1-2x1° , ,		I = [arcsin — l)]i = i^71
19.9.	/ =	^r[^ln JT^!,"^8'"^5'	19.10.

18.142.    / = i(4 + 3;c)³ln |a| — ^ ln |jc|— 1 6at-6at² — jc³

18.143.    / = jPf⁴ln|A² +3|—^(-jx⁴ —3a² + 91n|x² +3|).

18.144.    /=— (x——).

In a \ ln aj

19.11. / = [- jV3 + 4jr-4jr²+arcsin-i(l -2x)]J = 1 -2    .

19.12.    7=[4_N/5arcsiny^y5]^y^V=2._N/5(arcsin 1 -arcsin(—l)) = j^5n.

19.13.    / = [i(x³ + 3* + 1 )*]² = i (15* - 5^ł

19.14.

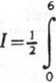
2 xdx , 4 +(x²)^2    2

[ln|x^J +V4 +x⁴ |]o = jln(18+5Vl3)-

19.15. / = [(Vx²+4n²)³J“₀ = (5_N/5-8)a³.

2 + J2

19.16. / = [2(x — \ )sj_x² — 2x— 1 — ln|x— 1 +\/x² -2x- 1 |]j=-|n/7 — J2 + ln ^

19.17.

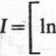
x + 2+2n/x²+x + iJi

T-

ln 5

3+2^3

6 WlTT

19.18.    / = [{*\Ja² -x² + -_ża² arcsin (x/u)]° = a².

19.19.    i = [4x³aictgx—ix²+jln(l+x²)]i=₁!₅7r-i + ^ln2.

2

19.20.    / = [e*-ln(l+<r^x)]² = e² —1+ln-.

1 +e

19.21. I = [—e~*(x + l)]J = —-2 +1.    19.22. / = [.v²-|^]² = 2e⁴-ie.

19.23. / = [-\e~ ^2x(x² + x+i)] I i=±e²(5e² -1).

19.24. I = [|e^2jc(2 - sin 2x- cos 2*)]+'=-i(3e* - 1).

19.25. / = [tg ±*]f=l.    19.26.

19.27. I = [sinjr—±sin³*]!£=f.

/= ln

2 + tgj* 2-tg i*

= ln3.

Jo

19.28.

19.29.

/V    -T    X.    Z*. i -L I    -T    -ł-    »    ^A

-+—^arctg-==—    =—— arctg-p-----_Farctg—=-.

3(2 + sinx) 3^3    73 Jo 3>/3    73 6    3^3    73

^ J" 1    1 ^ 72+7l +cos x"|^ł*

L71 +cosx 2yfl 71-71 +cos

, i , V2+i i i 72+71

= 1--= ln —=---=3--ln —=-—■

2V2 72-1 7| 272 72-71

19.30.    / = [j arctg i sin x]Ź”=± [arctg j- arctg ^].

19.31.    J=[cosx+lntg-jx]|3J= —-j+ln73•    19.32. / = [(* + !)sin*+cosx]o" = 5tt-

19.33. /=["—T =2(72-1).    19.34. / = [271 -l-sinjc]S* = 2(7^ — 1)-

Lcosxjo

19.35. /= [xtgx + lncos jr]5’^I=jn+ln-j72-

19.36. Przyjmujemy a>0. Obliczone pole wynosi ^a³ i stanowi \ wymienionego prostokąta. Warto zaznaczyć, że wynik ten znany już był Archimedesowi — na innej oczywiście drodze.

19.37. i.

19.39. P = 2 [2x² — jx⁴]² = 8. 19.41. p = [|*M*⁴]i = n-

19.38. §.

19.40. P = [⁴77³-|jc⁴]²=|.

19.42. P = 2[-±x³+fx² + lCbc]l₂ = 114|.