246

490 Rozwiązania i odpowiedzi

18.79. cosx#0, /=jarctg(tg²x), lub sinjc^O, /= -iarctg(ctg² x).

Wskazówka. Zakładając, że cosx#0, dzielimy licznik i mianownik funkcji podcal kowej przez cos⁴ x, a następnie podstawiamy tg² x = t\ drugą postać otrzymamy dzi_e|ą_c licznik i mianownik przez sin⁴ x i podstawiając ctg² x — t. Związek między tymi całkami wynika ze wzoru

a + b

arctg a+arctg 6 = arctg

1 — ab

1    1

a w szczególności ze wzoru arctg a + arctg—=-£it albo arctga + arctg — = — jn.

a    a

18.80. cosjt^O; / = 2tgx+|_N/2arctg(_N/2tgx). 1

18.81. / = -■

sin x — cos x

1    72 —sin2x

18.82. / = —7= ln V--

2^/2 J 2 + sin2x

Wskazówka (do zad. 18.82). Funkcję podcałkową wyrazić przez funkcję kąta podwójnego.

18.83.    /=jarctg(2tg²x + l).

3 /tg*

18.84.    1 =—-= arctg

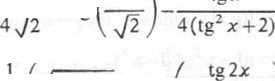
18.85. /= - l\/2 +JŻ arctg

74+172

18.86.    /=-j_N/2 arctg (\J2 tg 2x).

18.87.    cosjf^O; I tg x+^j2 arctg {Jl tg x).

18.91. i = jx²-\xj I — x² arcsin x + j(arcsin x)² . x arcsin x

18.92. — 1 <jc< 1 ; / =

TT

+ ±ln|l-*²|.

18.93.    / = xarctgln |l + *²|-|(arctgx)² .

18.94.    / = 3 TTctg3x .

f*-

(arctg x)³

18.96. 1 =-— .

18.95. / =

18.97. / = -

1

2 arcctg 2x 1

arccos x 2

18.98. I = ln |arcsin x| .

18.99. / =

(x— l)arctgx + x 4(1+x²)

arcsin x ,    1 — x

18.100. — 1 <x< l ; /= .. _+jln-

TTTc²

l+x

18.101.    -l<x<l; / =f(.x:²-f)arcsin*+3Wl-*².

18.102.    +

18.103.    / = ±x³arctgx-ix²+±ln|l+x²|.

18.104.    / = * — ln (1 + e^x) — 2e^ixarctge~^ix — (arctg| x)².

arcsin* . 1 + Vl—x²

18.105. — 1 <x<0 lub 0<x< 1 ; 1=---ln -j—,--

* |*|

18.106.    /=x-e^x arcsin e^x - ln (1 +VT+e²ⁱ) .

18.107.    /=i(*⁷arctg*—1*⁶+|*⁴—j*²+-jln|l+*²|) .

18.108.    1 <*<2 ; /= ~(2*+21)V-*²+3*-2 + (*²+3*-arccos(2*-3).

18.109.    I=\J 1 +*² arctg* —ln |* + %/l +*²| .

18.110.    -1<*<1 ; /= -g*²+3*n/T^T*²arcsin*+ g(arcsin*)² .

18.111.    /=3*+j^*³+|(1+*²)² arctg* .

_n    2 Jx

18.112.    —2 sin (1 -*) _N/*+(l+*) arcsin-.

1 +*

18.118. I=±e^3x+2Ve*.    18.119. / = ln(e^x + <T^x) = ln(cosh*).

. f sinh *

Wskazówka (do zad. 18.119). Całkę przedstawić w postaci _cos|_lx ***'

18.120. x*0; /=-jln \e^2x—\\ — x.    18.121. / = arctg e*.

18.122. / = 2Ve^J[ + l+ln^^e--ti— ■    18.123. 1 = 2 ln |e^x + l|-x.

Ve^x + l + l

Wskazówka (do zad. 18.122). Podstawić -Je* +1 = t.

_ło 1    V3+I7-V3    , ,-

18.124. / =-j= ln _-p.    18.125. /=-|V(l + e^x)³.

n/3    x/3+27 + V3    ³

Wskazówka (do zad. 18.124). Podstawić 3 + 2e^x = f².

-I    e^2x-«T^2x

18.126. I = -z—- ■    18.127. / ---+2*.

e — 1    2

Uwaga (do zad. 18.127). Można również całkę przedstawić w postaci 4 J cosh² * dx = = 2 sinh x cosh * + 2* (całkując przez części).