2tom235

6. NAPĘD ELEKTRYCZNY 472

a) c 25 Bu		/ V	b) s 2u
»e	mĄ/	i		A
	■ yr y		«a		r
0		i n 3? i 3?	M 0		tu t

Rys. 6.9. Stany dynamiczne napędu przy liniowych charakterystykach silnika i mechanizmu: a) moment mechaniczny M_m oraz moment silnika b) prędkości obrotowe przy przejściu napędu od S2_e do f?_u

Na rysunku 6.9a przedstawiono charakterystyki silnika i mechanizmu, a na rys. 6.9b — przebieg czasowy prędkości.

Podstawiając zależność (6.15) do równania charakterystyki silnika, otrzymuje się przebieg momentu elektromagnetycznego

M_e(t) = M,( 1 — e”'^/r-) + M_ea e^_,/T-    (6.17)

Na rysunku 6.10b pokazano przebieg czasowy momentu.

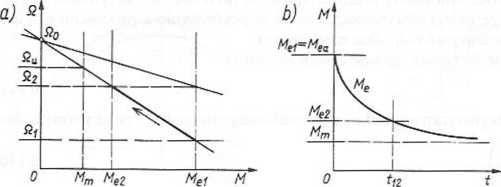
Rys. 6.10. Stan dynamiczny napędu przy zmianie prędkości od Qj do ft₂: ^a) momenty M_r oraz b) moment silnika M_e = /(r)

W uproszczonych obliczeniach najczęściej wielkością poszukiwaną jest czas trwania procesu przejściowego od prędkości Q_l do Q₂. Przy oznaczeniach jak na rys. 6.10a czas ten jest określony zależnością

t_t2=J

m

ln-

-M.

M.

■

(6.18)

Jeżeli Q₂ jest prędkością ustaloną przy M_e2 = M_m, to czas przebiegu będzie teoretycznie nieskończenie długi. Przyjmuje się wówczas, że stan przejściowy zakończy się przy Q₂ = 0.95 Q_u. Wówczas wzór (6.18) określa przy fJ, = 0 czas rozruchu

J

0,95 Q_u    1

ⁿ 0,05

37-

n„

M,

(6.19)

Dla silników indukcyjnych klatkowych napędzających mechanizmy o dużej bezwładności, czas rozruchu szacuje się przyjmując stalą wartość momentu elektromagnetycznego (jak na rys. 6.11). Moment wówczas wynika ze wzoru

Q_u

(6.20)

= const

M, = M.

M, + M„ 2

zaś czas rozruchu (wyrażony w sekundach)

Drogę rozruchu w mierze kątowej wylicza się jako całkę

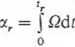
w prostym przypadku opisanym równaniem (6.20) droga rozruchu, wyrażona w radianach

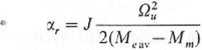
(6.21)

Czasy rozruchu napędów z silnikami małych i średnich mocy wynoszą od ułamka sekundy do kiku sekund, zaś odpowiadające im drogi kątowe wirnika mieszczą się między częścią pełnego obrotu 2n (wyrażonego w radianach) a kilkudziesięcioma pełnymi obrotami.

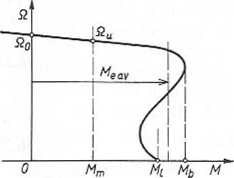
Rys. 6.11. Wyznaczenie czasu rozruchu silnika indukcyjnego klatkowego w napędzie z dużymi masami zamachowymi

W podobny sposób udaje się oszacować czasy trwania stanów przejściowych przy hamowaniu. Wówczas przebieg zawiera się między stanem początkowym = Q_u a stanem końcowym Q₂ = 0- Moment dynamiczny jest ujemny (hamujący) i stanowi sumę momentów

Równanie ruchu (6.20) będzie miało postać

(6.22)

Q_u

lkJ---

M_m+M_m

W przypadkach złożonych, gdy charakterystyka silnika lub mechanizmu jest dana w postaci wykresu lub tabeli i w dodatku moment bezwładności nie jest stały, najkorzystniej jest posłużyć się metodą małych przyrostów prędkości kąta obrotu oraz momentu bezwładności. Równanie ruchu zapisuje się wówczas dla k-tego odcinka czasu

M_dk = M_ek-M_mk = J_k-

ĄO*

A U

A Jk 2 A_h

(6.23)

Dla stałych przyrostów czasu At = const należy wyznaczać składową momentu dynamicznego od przyrostu prędkości oraz składową od przyrostu momentu bezwładności, a więc odpowiednio