2tom316

9. URZĄDZENIA DO KOMPENSACJI MOCY BIERNEJ 634

Moce te mogą być reprezentowane geometrycznie w postaci krawędzi czworościanu przedstawionego na rys. 9.1.

Czworościan mocy ma cztery kąty proste, zaś kąty pozostałe są określone przez

następujące związki:

— współczynnik mocy

P

cos cp - —    (9.14)

iJ

— współczynnik obciążenia

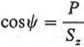
(9.15)

— współczynnik deformacji

(9.16)

cosy = —

S

przy czym

cos (p = cos 4/ cosy    (9.17)

Z zależności (9.17) wynika, że w celu poprawy współczynnika mocy należy zmniejszyć moc bierną i moc deformacji.

Kompensacja tylko mocy biernej <2_B — wyrażonej wzorem (9.9) — nie prowadzi do minimalizacji prądu źródła, gdyż moc ta może być równa zeru przy niezerowych wartościach mocy biernych poszczególnych harmonicznych (kompensacja każdej z nich oddzielnie jest niewykonalna).

W sieciach elektroenergetycznych średnich napięć współczynnik odkształcenia (niesi-nusoidalności) napięcia, zgodnie z przepisami [9.37] musi być ograniczony do wartości

wynikającej z zależności

o,05    (9-l«

U \

przy czym U_l — skuteczna wartość podstawowej harmonicznej napięcia.

Z wystarczającą w praktyce dokładnością można więc przyjąć, że odbiorniki energu są zasilane napięciem sinusoidalnym, tj. U & U _u a wyższe harmoniczne prądu są generowane przez ich elementy nieliniowe. Przy takim założeniu

P = UI₁cos<p₁;

(9.19)

Q_b = CZ/jSiną*!;

K = U

in

Poprawa współczynnika mocy (zmniejszenie mocy pozornej źródła) sprowadza się w praktyce nie tylko do kompensacji mocy biernej podstawowej, ale także do kompensacji mocy deformacji. Kompensacja mocy deformacji K (9.19) polega na odciążeniu sieci zasilającej i źródła od przepływu wyższych harmonicznych prądu generowanych przez odbiornik energii.

Wobec braku wyższych harmonicznych w napięciu, harmoniczne prądu mogą być filtrowane za pomocą poprzecznych filtrów LC (por. p. 9.6).

Inny sposób rozkładu mocy pozornej odbiornika jednofazowego zaproponował S. Fryzę [9.10].

Z czasowego przebiegu prądu i(r) można wyodrębnić składową czynną

i,(t) = -j^-u(r) = Gu(t)    (9.20)

i składową bierną

(9.21)

(9.22)

Składowa czynna (9.20) spełnia równanie mocy odbiornika

1!

F = —j u(t)i(t)dt = — J u(t)i_p(t)dt

¹ O    ¹ 0

stąd

f “(0«,(0 df = -771 ip(t)i_q(t)dt = 0 o    -*o

Oznacza to, że tak określony prąd bierny (9.21) jest ortogonalny do składowej czynnej prądu (9.20), czyli

I² = I²P + I²    (9.23)

a tym samym

S² = P² + Qj    (9.24)

Pomiędzy mocą bierną Q_B i Q_r istnieje następujący związek:

Q²F = Ql+K² = D²    (9.25)

Z zależności (9.21) wynika, że kompensacja mocy biernej polega na wywołaniu prądu — i_q(t) i może być zrealizowana w różny sposób.

9.1.2. Jednofazowe liniowe i nieliniowe odbiorniki mocy biernej

Odbiornik jednofazowy zasilany napięciem sinusoidalnym u(t) = Jl U sincur, którego prąd i(t) jest okresowy, wg C. J. Budeanu obciąża źródło mocą bierną

Q =

Ul 1, =

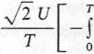
i(t)cosa>tdt

(9.26)

Znak minus przed całką określającą podstawową harmoniczną prądu wynika z przyjętej umowy, że moc bierna elementu indukcyjnego jest dodatnia, du    j—

Po uwzględnieniu, że — = (o-J2 U cos rot, otrzymuje się

1

1

Q = —Ou di = — — C )/du

2it

2tt

(9.27)