364 365

364

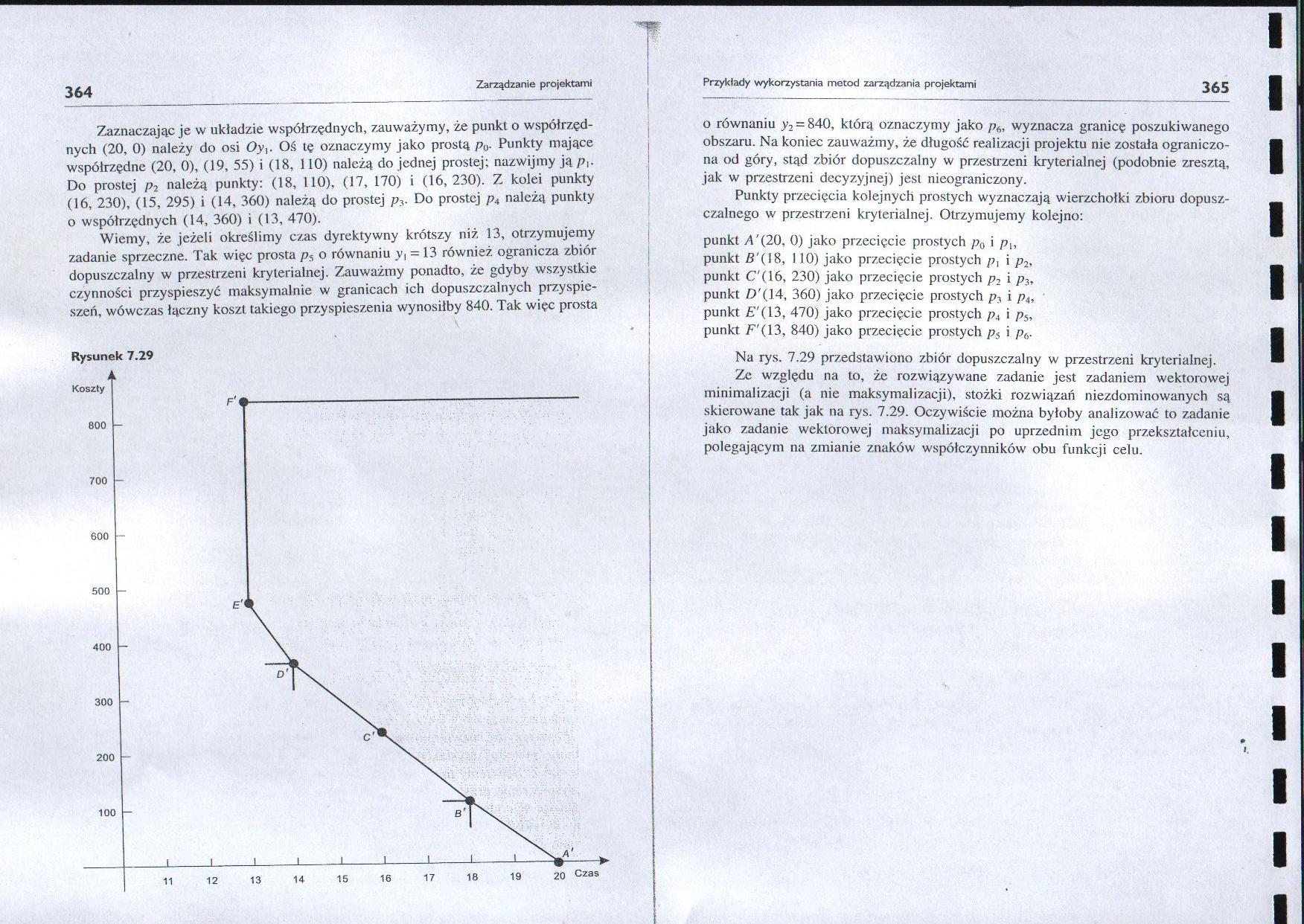
Zaznaczając je w układzie współrzędnych, zauważymy, że punkt o współrzędnych (20, 0) należy do osi Oy,. Oś tę oznaczymy jako prostą p_u. Punkty mające współrzędne (20, 0), (19, 55) i (18, 110) należą do jednej prostej; nazwijmy ją /?,. Do prostej p₂ należą punkty: (18, 110), (17, 170) i (16,230). Z kolei punkty (16, 230), (15, 295) i (14, 360) należą do prostej p,. Do prostej p_Ą należą punkty o współrzędnych (14, 360) i (13, 470).

Wiemy, że jeżeli określimy czas dyrektywny krótszy niż 13, otrzymujemy zadanie sprzeczne. Tak więc prosta p₅ o równaniu y₍ = 13 również ogranicza zbiór dopuszczalny w przestrzeni krylerialnej. Zauważmy ponadto, że gdyby wszystkie czynności przyspieszyć maksymalnie w granicach ich dopuszczalnych przyspieszeń, wówczas łączny koszt takiego przyspieszenia wynosiłby 840. Tak więc prosta

Rysunek 7.29 A

Koszty

800 700 600

500

400

300

200

100

I    I _1__I__I_____U--1----_H

13    14    15    16    17    18    19    20 ^Czas

►

11

12

Przykłady wykorzystania metod zarządzania projektami

365

o równaniu v₂ = 840, którą oznaczymy jako p_h, wyznacza granicę poszukiwanego obszaru. Na koniec zauważmy, że długość realizacji projektu nie została ograniczona od góry, stąd zbiór dopuszczalny w przestrzeni kryterialnej (podobnie zresztą, jak w przestrzeni decyzyjnej) jest nieograniczony.

Punkty przecięcia kolejnych prostych wyznaczają wierzchołki zbioru dopuszczalnego w przestrzeni kryterialnej. Otrzymujemy kolejno:

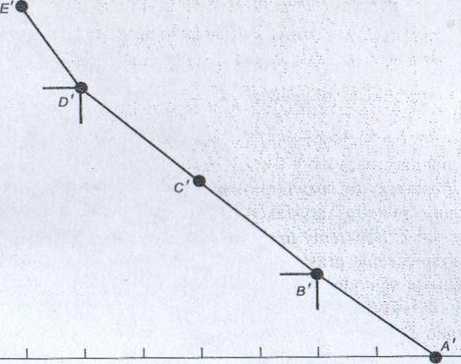
punkt A\20, 0) jako przecięcie prostych p₀ i /?,, punkt B'(18, 110) jako przecięcie prostych /?, i p₂, punkt C'(16, 230) jako przecięcie prostych p₂ i p₃, punkt £>'(14. 360) jako przecięcie prostych p₃ i p₄, punkt £'(13, 470) jako przecięcie prostych p_Ą i p₅, punkt F'(13, 840) jako przecięcie prostych p_s i p_b.

Na rys. 7.29 przedstawiono zbiór dopuszczalny w przestrzeni kryterialnej.

Ze względu na to, że rozwiązywane zadanie jest zadaniem wektorowej minimalizacji (a nie maksymalizacji), stożki rozwiązań niezdominowanych są skierowane tak jak na rys. 7.29. Oczywiście można byłoby analizować to zadanie jako zadanie wektorowej maksymalizacji po uprzednim jego przekształceniu, polegającym na zmianie znaków współczynników obu funkcji celu.