0554

556

XIII. Całki niewłaściwe

Łatwo można zauważyć, że gdy x -► 0, funkcja podcałkowa dąży do 0, a więc funkcję tę można uważać za ciągłą w całym przedziale całkowania, lecz już pierwsza pochodna funkcji podcałkowej jest w punkcie x =» 0 nieskończona. Korzystając z rozwinięcia logarytmu przedstawimy naszą funkcję w postaci sumy dwóch funkcji

g(x) = ln x-

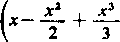
4

■)

<p(x) = In x-

ln (1+jc)-

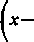
*1

2

x^_

4

)]•

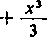
Całkę z pierwszej funkcji można łatwo obliczyć: wartość jej wynosi —0,20528... Całkę z drugiej funkcji (która ma już cztery pochodne ciągłe) obliczamy według wzo.ru Simpsona (2n = 10, pięć cyfr po przecinku). Otrzymamy —0,00348, a więc wynik ostateczny wynosi —0,20876.

Ponieważ |ęj^<4)(*)|<36 więc |R| <0,00002. Ostatecznie

i/| — 0,20876_±o,00003 — 0,2087+o,oooi ■

(W rzeczywistości wszystkie otrzymane cyfry tej wartości przybliżonej są dokładne, ponieważ prawdziwa wartość I wynosi —0,2087618...).

Ciekawe, że gdy wzór Simpsona (dla tej samej wartości 2n = 10 i obliczając tak samo do pięciu cyfr po przecinku) zastosujemy do funkcji podcałkowej bez uprzedniego wydzielenia osobliwości, otrzymamy /« —0,2080, tzn. otrzymamy tylko trzy dokładne cyfry po przecinku.

Tak więc, jeżeli nie skorzystamy z wydzielenia osobliwości, to nie tylko będziemy mieli trudności z oszacowaniem błędu, lecz możemy nawet faktycznie uzyskać mniejszą dokładność wyniku.

501. Przybliżone obliczanie całek niewłaściwych w przedziale nieskończonym. Rzadko udaje się obli-

+•    A

czyć całkę ff(x) dx na podstawie jej definicji jako granicę całki właściwej /f(x) dx przyjmując w przybli-

•    a

4 oo A

żeniu dla dostatecznie dużego A, że / « / i obliczając znanymi metodami tę ostatnią całkę. Może się to

a a

okazać korzystne tylko wtedy, gdy funkcja podcałkowa szybko maleje wraz ze wzrostem x, tzn, wtedy, gdy nawet przy niedużym A podana poprzednio przybliżona równość jest już wystarczająco dokładna.

<0 ₂

1) Tak będzie na przykład w przypadku całki / « J e~^x dx.

o

Z nierówności x² > 2Ax—A² wynika, że

e~^xl<e^Al ■ e~^IAx

oraz

J e~**dx < e^A* • f e~^2Axdx =—1—e~^A*.

A    A    ^2A

Dla A = 3 jest

00

(' e~^xldx < 0,00002 .

3

3

Całkę J e~'²dx obliczamy według wzoru Simpsona biorąc n = 30 i uwzględniając w obliczeniach o

pięć cyfr po przecinku. Otrzymujemy 0,88621. Łatwo otrzymujemy oszacowanie !(<?-*⁵)^<4>|<12, |J?|< <2-10^-5. Ogólny błąd zawarty jest między —0,00004 i 0,00006. A więc

0,88617 < / < 0,88627,    / = 0,8862_±o ,0001 •

Jak wiemy [492, 2°], dokładna wartość I wynosi ]/7t/2 = 0,886226...