33327 PC043387

1. Repety®®

Przykład 1.78

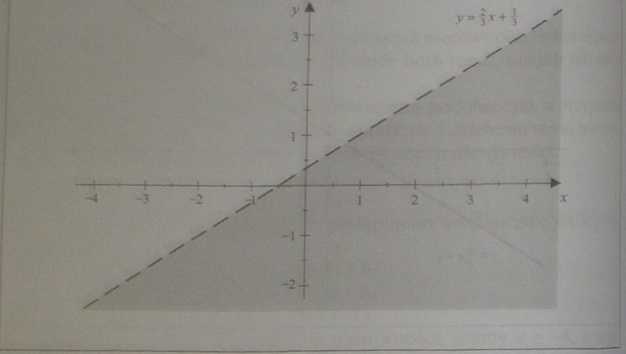
Aby zaznaczyć w układzie współrzędnych zbiór rozwiązań nierównoSjj 2fc - 3y + 1 > 0, przekształcamy ją dó postaci y < 4 x + i. Następnie szkicuje® prosta o równaniu y = - x + j. Szukany obszar tó część płaszczyzny znajdują się poniżej (bo w nierówności jest    tej prostej (por. ilustracja 1.40)

Punkty leżące na pros tej nie należą do zbioru rozwiązań (bo nierówność^ silna), diatógo prostą zaznaczyliśmy linią przerywaną.

Ilustracja 1.40. Interpretacja graficzna rozwiązania nierówności 2x - 3y + 1 > 0

. --------------- -------—»*«*.

Układy równań i nierówności liniowych

Definicja 1.69. Układ równań

gdzie a,^z + bf * 0 oraz a{ + h} * 0, nazywamy układem dwóch równań liniowych z dwiema niewiadomymi x iy.

j

W zależńóśći od stałych a,. h,, a₂ i 65 okład równań (1.8) może być:

-    oznaczony, gdy posiada dokładnie jedno rozwiązanie (rozwiązaniem jest jedna para liczb),

-    nieoznaczony, gdy posiada nieskończenie wiele rozwiązań (rozwiązania leżą na prostej),

-    sprzeczny, gdy nie posiada rozwiązania.

Istnieje kilka metod rozwiązywania układów równań postaci (1.8), m.ift.: metoda eliminacji {podstawiania), metoda przeciwnych współczynników, metoda graficzna (przybliżona), metoda wyznaczników (twierdzenie Ćramera), metoda wykorzystująca pojęcie macierzy odwrotnej.

W tej części omówimy trzy pierwsze metody. Pozostałe zostaną szczegółowo przedstawione w rozdziale 2.

Metoda eliminacji (podstawiania)

W metodzie tej Stosujemy następujący algorytm:

1)    Z wybranego równania wyznaczamy jedną z niewiadomych w zależności od drugiej niewiadomej.

2)    Otrzymaną zależność wstawiamy do drugiego równania, które staje się równaniem z jedną niewiadomą.

§f Rozwiązujemy to równanie, uzyskując jedną ze współrzędnych rozwiązania.

4) Wyznaczoną liczbę podstawiamy do pierwszego równania, otrzymując drugą ze współrzędnych rozwiązania.

Przykład 1.79

|% 2y =.'9    --    ■ y

Rozwiązując układ <    metodą podstawiania, z drugiego równania wy-

5x -2y=9 y*=l—3x

3x+y=l

. Następnie zay w pierwszym

znaczymy niewiadomąy, otrzymując

15x-2(l-3x)=9

równaniu podstawiamy 1 -3x i uzyskujemy układ |

fx=l ' ' JtiS

Rozwiązując pierwsze równanie, otrzymujemy j _    . - Uzyskaną war-

tość podstawiamy zax do równania drugiego, otrzymując rozwiązanie układu postaci: x = 1, y = -2.