406 407

406 Programowanie dynamiczne

9.2.4. Zasada optymalności Bellmana i równania optymalności

Rozwiązując zadanie metodą programowania dynamicznego, wykorzystamy zasadę optymalności Bellmana. W ślad za jej twórcą możemy sformułować ją następująco:

Zasada optymalności

Strategia optymalna ma tą własność, że niezależnie od stanu początkowego i decyzji początkowej, pozostałe decyzje muszą stanowić ciąg optymalny ze wzglądu na stan wynikający z pierwszej decyzji-

Zasada optymalności pozwala na dekompozycję zadania wyjściowego na ciąg powiązanych ze. sobą prostszych zadań, które rozwiązujemy kolejno, rozpoczynając od ostatniego etapu.

Rozpatrzymy kolejne stany dla etapu 3 (rys. 9.3).

Rysunek 9.3

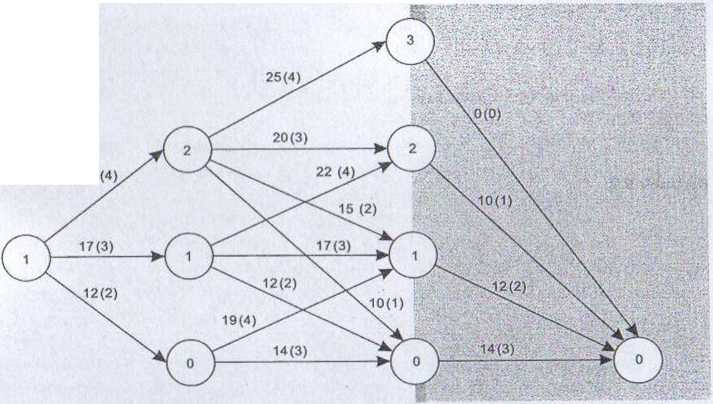
Przypuśćmy, że na początku ostatniego, trzeciego etapu proces znalazł się w stanie y, = 0. Chcąc określić optymalny sposób postępowania w zaistniałej sytuacji, zgodnie z zasadą optymalności wybieramy taką decyzję, aby sterowanie przebiegiem procesu od stanu y₃ = 0 do końca procesu było optymalne. Tę optymalną wartość, oznaczoną jako gt(0). otrzymujemy przez rozwiązanie następującego równania optymalności:

gf (0) = min 114) = 14, czyli gt(0)= 14.

Metoda programowania dynamicznego

Optymalnym sposobem działania dla stanu y.? = 0, będącym częścią poszukiwanej przez nas strategii optymalnej, jest decyzja X*, - 3, co zapisujemy następująco:

x?(0) = 3.

Zapisujemy dalsze równania optymalności dla kolejnych stanów etapu 3: £*(1) = min {12}, czyli gf(l) = 12.

Tak więc optymalnym sposobem działania dla stanu y₃ = 1 jest decyzja xf (1) = 2.

!

Otrzymujemy kolejno: gf (2) = min {10}, czyli g?(2) = 10, oraz xf (2) = I,

g$(3) = min {0}, czyli gf(3) = 0, oraz x?(3) = 0.

Obecnie zajmiemy się konstrukcją równań optymalności dla kolejnych stanów etapu 2. W tym celu będziemy minimalizowali sumę kosztów związanych z realizacją procesu od kolejnych stanów etapu drugiego do końca procesu (rys. 9.4).

Każda taka suma składa się z dwóch składników. Pierwszy z nich to koszty związane ze sterowaniem procesem w rozpatrywanym etapie (czyli w etapie 2), natomiast drugi to minimalne koszty sterowania procesem w etapach pozostałych

Rysunek 9.4

²²

9a(0)⁼ 14